
【题目】已知:如图,四边形ABCD中,对角线AC,BD相交于点O,AB=AC=AD,∠DAC=∠ABC. 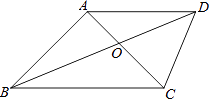
(1)求证:BD平分∠ABC;
(2)若∠DAC=45°,OA=1,求OC的长.
【答案】
(1)解:证明:∵AB=AC,
∴∠ABC=∠ACB,
∵∠DAC=∠ABC,
∴∠DAC=∠ACB.
∴AD∥BC,
∴∠ADB=∠CBD.
又∵AB=AD,
∴∠ADB=∠ABD.
∴∠ABD=∠CBD.
∴BD平分∠ABC;
(2)解:解:过点O作OE⊥BC于E,
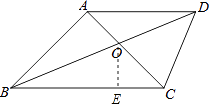
∵∠DAC=45°,∠DAC=∠ABC,
∴∠ABC=∠ACB=45°,
∴∠B AC=90°,
∵BD平分∠ABC,
∴OE=OA=1.
在Rt△OEC中,∠ACB=45°,OE=1,
∴OC= ![]() .
.
【解析】(1)根据等腰三角形的性质、平行线的性质以及角平分线的定义证明;(2)过点O作OE⊥BC于E,根据角平分线的性质得到OE=OA,根据勾股定理计算即可.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两校参加区教育局举办的学生英语口语竞赛,两校参赛人数相等.比赛结束后,发现学生成绩分别为7分、8分、9分、10分(满分为10分).依据统计数据绘制了如下尚不完整的统计图表.
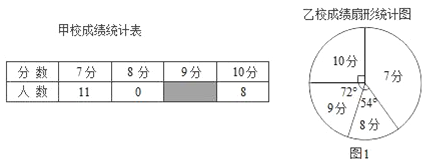
(1)在图1中,“7分”所在扇形的圆心角等于 °.
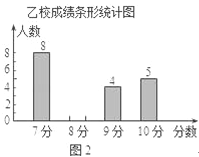
(2)请你将图2的统计图补充完整;
(3)经计算,乙校的平均分是8.3分,中位数是8分,请写出甲校的平均分、中位数;并从平均分和中位数的角度分析哪个学校成绩较好.
(4)如果该教育局要组织8人的代表队参加市级团体赛,为便于管理,决定从这两所学校中的一所挑选参赛选手,请你分析,应选哪所学校?
查看答案和解析>>
科目:初中数学 来源: 题型:
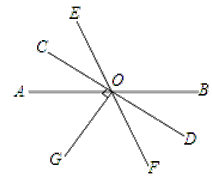
【题目】如图,已知直线AB、CD、EF相交于点O,OG⊥CD,∠BOD=36°.
(1)求∠AOG的度数;
(2)若OG是∠AOF的平分线,那么OC是∠AOE的平分线吗?说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某“数学兴趣小组”根据学习函数的经验,对函数y= ![]() 的图象和性质进行了探究,探究过程如下,请补充完整:
的图象和性质进行了探究,探究过程如下,请补充完整: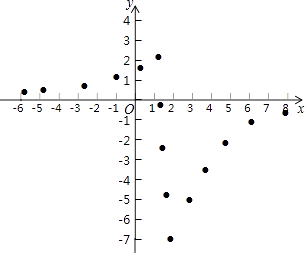
(1)该函数的自变量x的取值范围是;
(2)同学们先找到y与x的几组对应值,然后在下图的平面直角坐标系xOy中,描出各对对应值为坐标的点.请你根据描出的点,画出该函数的图象;
(3)结合画出的函数图象,写出该函数的一条性质: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国古代有二十四节气歌,“春雨惊春清谷天,夏满芒夏暑相连.秋处露秋寒霜降,冬雪雪冬小大寒.”它是为便于记忆我国古时历法中二十四节气而编成的小诗歌,流传至今.节气指二十四时节和气候,是中国古代订立的一种用来指导农事的补充历法,是中国古代劳动人民长期经验的积累和智慧的结晶.其中第一个字“春”是指立春,为春季的开始,但在气象学上的入春日是有严格定义的,即连续5天的日平均气温稳定超过10℃又低于22℃,才算是进入春天,其中,5天中的第一天即为入春日.例如:2014年3月13日至18日,北京的日平均气温分别为9.3℃,11.7℃,12.7℃,11.7℃,12.7℃和12.3℃,即从3月14日开始,北京日平均气温已连续5天稳定超过10℃,达到了气象学意义上的入春标准.因此可以说2014年3月14日为北京的入春日. 日平均温度是指一天24小时的平均温度.气象学上通常用一天中的2时、8时、14时、20时4个时刻的气温的平均值作为这一天的日平均气温(即4个气温相加除以4),结果保留一位小数.
如表是北京顺义2017年3月28日至4月3日的气温记录及日平均气温(单位:℃)
时间 | 2时 | 8时 | 14时 | 20时 | 平均气温 |
3月28日 | 6 | 8 | 13 | 11 | 9.5 |
3月29日 | 7 | 6 | 17 | 14 | a |
3月30日 | 7 | 9 | 15 | 12 | 10.8 |
3月31日 | 8 | 10 | 19 | 13 | 12.5 |
4月1日 | 8 | 7 | 18 | 15 | 12 |
4月2日 | 11 | 7 | 22 | 16 | 14 |
4月3日 | 13 | 11 | 21 | 17 | 15.5 |
根据以上材料解答下列问题:
(1)求出3月29日的日平均气温a;
(2)采用适当的统计图将这7天的日平均气温的变化情况表示出来;
(3)请指出2017年的哪一天是北京顺义在气象学意义上的入春日.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形ABCD在第一象限内,边BC与x轴平行,A,B两点的纵坐标分别为3,1,反比例函数y= ![]() 的图象经过A,B两点,则菱形ABCD的面积为( )
的图象经过A,B两点,则菱形ABCD的面积为( ) 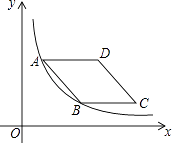
A.2
B.4
C.2 ![]()
D.4 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,D是函数y= ![]() (k>0,x>0)图象上两点(点A在点D的左侧),直线AD分别交x,y轴于点E,F.AB⊥x轴于点B,CD⊥x轴于点C,连结AO,BD.若BC=OB+CE,S△AOF+S△CDE=1,则S△ABD= .
(k>0,x>0)图象上两点(点A在点D的左侧),直线AD分别交x,y轴于点E,F.AB⊥x轴于点B,CD⊥x轴于点C,连结AO,BD.若BC=OB+CE,S△AOF+S△CDE=1,则S△ABD= . 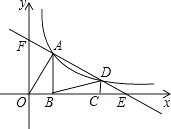
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com