练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在平面直角坐标系中，菱形ABCD在第一象限内，边BC与x轴平行，A，B两点的纵坐标分别为3，1，反比例函数y= 的图象经过A，B两点，则菱形ABCD的面积为（ ）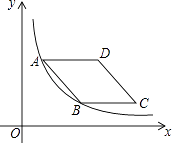
    A.2
    B.4
    C.2
    D.4

    【答案】D
    【解析】解：∵点A、B在反比例函数y= 的图象上，且A，B两点的纵坐标分别为3、1， ∴点A（1，3），点B（3，1），
    ∴AB= =2 ．
    ∵四边形ABCD为菱形，BC与x轴平行，
    ∴BC=AB=2 ，
    ∴S菱形ABCD=BC（yA﹣yB）=2 ×（3﹣1）=4 ．
    故选D．
    【考点精析】通过灵活运用菱形的性质，掌握菱形的四条边都相等；菱形的对角线互相垂直，并且每一条对角线平分一组对角；菱形被两条对角线分成四个全等的直角三角形；菱形的面积等于两条对角线长的积的一半即可以解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

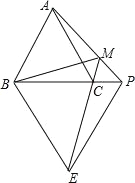
    【题目】如图，已知等边△ABC 和等边△BPE，点 P 在 BC 的延长线上，EC 的延长线交 AP 于点 M，连接 BM；下列结论：①AP＝CE；②∠PME＝60°；③BM 平分∠AME；④AM+MC＝BM，其中正确的有____________________（填序号）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（探究）如图①，∠AFH和∠CHF的平分线交于点O，EG经过点O且平行于FH，分别与AB、CD交于点E、G．

    (1)若∠AFH＝60°，∠CHF＝50°，则∠EOF＝_____度，∠FOH＝_____度．

    (2)若∠AFH+∠CHF＝100°，求∠FOH的度数．

    （拓展）如图②，∠AFH和∠CHI的平分线交于点O，EG经过点O且平行于FH，分别与AB、CD交于点E、G．若∠AFH+∠CHF＝α，直接写出∠FOH的度数．(用含a的代数式表示)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，四边形ABCD中，对角线AC，BD相交于点O，AB=AC=AD，∠DAC=∠ABC．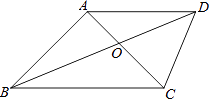
    （1）求证：BD平分∠ABC；
    （2）若∠DAC=45°，OA=1，求OC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

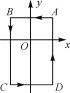
    【题目】如图，在平面直角坐标系中：A(1，1)，B(－1，1)，C(－1，－2)，D(1，－2)，现把一条长为2 018个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处，并按A→B→C→D→A→…的规律紧绕在四边形ABCD的边上，则细线另一端所在位置的点的坐标是________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

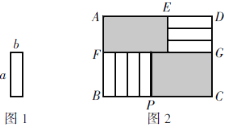
    【题目】将7张如图1所示的长为a，宽为b(a>b)的小长方形纸片按图2所示的方式不重叠地放在长方形ABCD内，未被覆盖的部分(两个长方形)用阴影表示．设左上角与右下角的阴影部分的面积的差为S，当BC的长度变化时，按照同样的放置方式，S始终保持不变，求a，b满足的条件．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，在△ABC中，∠A∶∠ABC∶∠ACB=3∶4∶5，BD，CE分别是边AC，AB上的高，BD，CE相交于H，求∠BHC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，不添加辅助线，请写出一个能判断EB∥AC的条件：___________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，∠BAD＝∠CAE＝90°，AB＝AD，AE＝AC.

    (1)证明：BC=DE；

    (2)若AC＝12，求四边形ABCD的面积.

    查看答案和解析>>

    同步练习册答案