
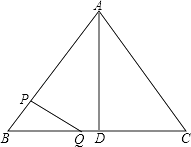
【题目】如图△ABC中,AB=AC=10厘米,BC=12厘米,D是BC的中点,点P从B出发,以a厘米/秒(a>0)的速度沿BA匀速向点A运动,点Q同时以1厘米/秒的速度从D出发,沿DB匀速向点B运动,其中一个动点到达端点时,另一个动点也随之停止运动,设它们运动的时间为t秒.
(1)若a=2,△BPQ∽△BDA,求t的值;
(2)设点M在AC上,四边形PQCM为平行四边形. ①若a= ![]() ,求PQ的长;
,求PQ的长;
②是否存在实数a,使得点P在∠ACB的平分线上?若存在,请求出a的值;若不存在,请说明理由.
【答案】
(1)解:△ABC中,AB=AC=10cm,BC=12cm,D是BC的中点,
∴BD=CD= ![]() BC=6cm,
BC=6cm,
∵a=2,
∴BP=2tcm,DQ=tcm,
∴BQ=BD﹣QD=6﹣t(cm),
∵△BPQ∽△BDA,
∴ ![]() ,
,
即 ![]() ,
,
解得:t= ![]()
(2)解:①过点P作PE⊥BC于E,
∵四边形PQCM为平行四边形,
∴PM∥CQ,PQ∥CM,PQ=CM,
∴PB:AB=CM:AC,
∵AB=AC,
∴PB=CM,
∴PB=PQ,
∴BE= ![]() BQ=
BQ= ![]() (6﹣t)cm,
(6﹣t)cm,
∵a= ![]() ,
,
∴PB= ![]() tcm,
tcm,
∵AD⊥BC,
∴PE∥AD,
∴PB:AB=BE:BD,
即 ![]() ,
,
解得:t= ![]() ,
,
∴PQ=PB= ![]() t=
t= ![]() (cm);
(cm);
②不存在.理由如下:
∵四边形PQCM为平行四边形,
∴PM∥CQ,PQ∥CM,PQ=CM,
∴PB:AB=CM:AC,
∵AB=AC,∴PB=CM,∴PB=PQ.
若点P在∠ACB的平分线上,则∠PCQ=∠PCM,
∵PM∥CQ,
∴∠PCQ=∠CPM,
∴∠CPM=∠PCM,
∴PM=CM,
∴四边形PQCM是菱形,
∴PQ=CQ,PM∥CQ,
∴PB=CQ,PM:BC=AP:AB,
∵PB=atcm,CQ=CD+QD=6+t(cm),
∴PM=CQ=6+t(cm),AP=AB﹣PB=10﹣at(cm),
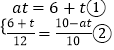 ,
,
化简得②:6at+5t=30③,
把①代入③得,t=﹣ ![]() ,
,
∴不存在实数a,使得点P在∠ACB的平分线上.
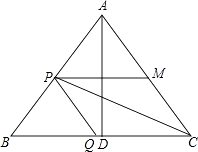
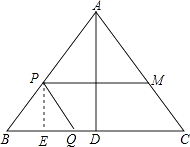
【解析】(1)由△ABC中,AB=AC=10厘米,BC=12厘米,D是BC的中点,根据等腰三角形三线合一的性质,即可求得BD与CD的长,又由a=2,△BPQ∽△BDA,利用相似三角形的对应边成比例,即可求得t的值;(2)①首先过点P作PE⊥BC于E,由四边形PQCM为平行四边形,易证得PB=PQ,又由平行线分线段成比例定理,即可得方程 ![]() ,解此方程即可求得答案;②首先假设存在点P在∠ACB的平分线上,由四边形PQCM为平行四边形,可得四边形PQCM是菱形,即可得PB=CQ,PM:BC=AP:PB,及可得方程组,解此方程组求得t值为负,故可得不存在.
,解此方程即可求得答案;②首先假设存在点P在∠ACB的平分线上,由四边形PQCM为平行四边形,可得四边形PQCM是菱形,即可得PB=CQ,PM:BC=AP:PB,及可得方程组,解此方程组求得t值为负,故可得不存在.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】2011年徐州市全年实现地区生产总值3551.65亿元,按可比价格计算,比上年增长13.5%,经济平稳较快增长.其中,第一产业、第二产业、第三产业增加值与增长率情况如图所示: 
根据图中信息,写成下列填空:
(1)第三产业的增加值为亿元:
(2)第三产业的增长率是第一产业增长率的倍(精确到0.1);
(3)三个产业中第产业的增长最快.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘核潜艇在海面DF下600米A点处测得俯角为30°正前方的海底C点处有黑匣子,继续在同一深度直线航行1464米到B点处测得正前方C点处的俯角为45°.求海底C点处距离海面DF的深度(结果精确到个位,参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732,
≈1.732, ![]() ≈2.236)
≈2.236)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数的图象与x轴相交于点A(﹣3,0)、B(﹣1,0),与y轴相交于点C(0,3),点P是该图象上的动点;一次函数y=kx﹣4k(k≠0)的图象过点P交x轴于点Q.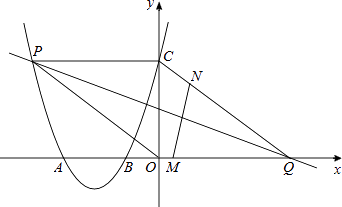
(1)求该二次函数的解析式;
(2)当点P的坐标为(﹣4,m)时,求证:∠OPC=∠AQC;
(3)点M,N分别在线段AQ、CQ上,点M以每秒3个单位长度的速度从点A向点Q运动,同时,点N以每秒1个单位长度的速度从点C向点Q运动,当点M,N中有一点到达Q点时,两点同时停止运动,设运动时间为t秒.
①连接AN,当△AMN的面积最大时,求t的值;
②直线PQ能否垂直平分线段MN?若能,请求出此时点P的坐标;若不能,请说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某测量船位于海岛P的北偏西60°方向,距离海岛100海里的A处,它沿正南方向航行一段时间后,到达位于海岛P的西南方向上的B处,求测量船从A处航行到B处的路程(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,规定把一个三角形先沿着x轴翻折,再向右平移2个单位称为1次变换.如图,已知等边三角形ABC的顶点B、C的坐标分别是(﹣1,﹣1)、(﹣3,﹣1),把△ABC经过连续9次这样的变换得到△A′B′C′,则点A的对应点A′的坐标是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某玩具由一个圆形区域和一个扇形区域组成,如图,在⊙O1和扇形O2CD中,⊙O1与O2C、O2D分别切于点A、B,已知∠CO2D=60°,E、F是直线O1O2与⊙O1、扇形O2CD的两个交点,且EF=24cm,设⊙O1的半径为xcm. 
(1)用含x的代数式表示扇形O2CD的半径;
(2)若⊙O1和扇形O2CD两个区域的制作成本分别为0.45元/cm2和0.06元/cm2 , 当⊙O1的半径为多少时,该玩具的制作成本最小?
查看答案和解析>>
科目:初中数学 来源: 题型:
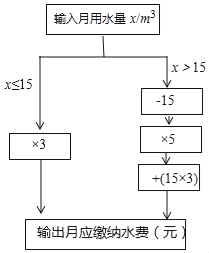
【题目】小明根据市自来水公司的居民用水收费标准,制定了水费计算数值转换机的示意图.(用水量单位:m3,水费单位:元)
(1)根据转换机程序计算下列各户月应缴纳水费
用户 | 张大爷 | 王阿姨 | 小明家 |
月用水量/m3 | 6 | 15 | 17 |
月应缴纳水费/元 |
|
|
|
(2)当x>15时,用含x的代数式表示水费 ;
(3)小丽家10月份水费是70元,小丽家10月份用水 m3.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是正三角形ABC内的一点,且PA=5,PB=12,PC=13,若将△PAC绕点A逆时针旋转后,得到△P′AB,求点P与点P′之间的距离及∠APB的度数. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com