
【题目】如图,二次函数的图象与x轴相交于点A(﹣3,0)、B(﹣1,0),与y轴相交于点C(0,3),点P是该图象上的动点;一次函数y=kx﹣4k(k≠0)的图象过点P交x轴于点Q.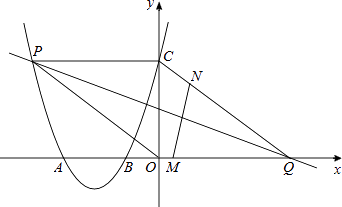
(1)求该二次函数的解析式;
(2)当点P的坐标为(﹣4,m)时,求证:∠OPC=∠AQC;
(3)点M,N分别在线段AQ、CQ上,点M以每秒3个单位长度的速度从点A向点Q运动,同时,点N以每秒1个单位长度的速度从点C向点Q运动,当点M,N中有一点到达Q点时,两点同时停止运动,设运动时间为t秒.
①连接AN,当△AMN的面积最大时,求t的值;
②直线PQ能否垂直平分线段MN?若能,请求出此时点P的坐标;若不能,请说明你的理由.
【答案】
(1)
解:设抛物线的解析式为:y=a(x+3)(x+1),
∵抛物线经过点C(0,3),
∴3=a×3×1,解得a=1.
∴抛物线的解析式为:y=(x+3)(x+1)=x2+4x+3
(2)
证明:在抛物线解析式y=x2+4x+3中,当x=﹣4时,y=3,∴P(﹣4,3).
∵P(﹣4,3),C(0,3),
∴PC=4,PC∥x轴.
∵一次函数y=kx﹣4k(k≠0)的图象交x轴于点Q,当y=0时,x=4,
∴Q(4,0),OQ=4.
∴PC=OQ,又∵PC∥x轴,
∴四边形POQC是平行四边形,
∴∠OPC=∠AQC
(3)
解:①在Rt△COQ中,OC=3,OQ=4,由勾股定理得:CQ=5.
如答图1所示,过点N作ND⊥x轴于点D,则ND∥OC,
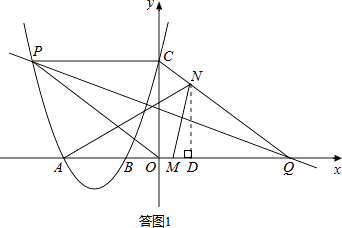
∴△QND∽△QCO,
∴ ![]() ,即
,即 ![]() ,解得:ND=3﹣
,解得:ND=3﹣ ![]() t.
t.
设S=S△AMN,则:
S= ![]() AMND=
AMND= ![]() 3t(3﹣
3t(3﹣ ![]() t)=﹣
t)=﹣ ![]() (t﹣
(t﹣ ![]() )2+
)2+ ![]() .
.
又∵AQ=7,∴点M到达终点的时间为t= ![]() ,
,
∴S=﹣ ![]() (t﹣
(t﹣ ![]() )2+
)2+ ![]() (0<t≤
(0<t≤ ![]() ).
).
∵﹣ ![]() <0,
<0, ![]() <
< ![]() ,且x<
,且x< ![]() 时,y随x的增大而增大,
时,y随x的增大而增大,
t=2.5时已超过运动时间又因为开口向下所以取 ![]() ,
,
∴当t= ![]() 时,△AMN的面积最大.
时,△AMN的面积最大.
②假设直线PQ能够垂直平分线段MN,则有QM=QN,且PQ⊥MN,PQ平分∠AQC.
由QM=QN,得:7﹣3t=5﹣t,解得t=1.
设P(x,x2+4x+3),
若直线PQ⊥MN,则:过P作直线PE⊥x轴,垂足为E,
则△PEQ∽△MDN,
∴ ![]() ,
,
∴ 
∴x= ![]() ,
,
∴P( ![]() ,
, ![]() )或(
)或( ![]() ,
, ![]() )
)
∴直线PQ能垂直平分线段MN
【解析】(1)利用交点式求出抛物线的解析式;(2)证明四边形POQC是平行四边形,则结论得证;(3)①求出△AMN面积的表达式,利用二次函数的性质,求出△AMN面积最大时t的值.注意:由于自变量取值范围的限制,二次函数并不是在对称轴处取得最大值;②直线PQ上的点到∠AQC两边的距离相等,则直线PQ能平分∠AQC,所以直线PQ能垂直平分线段MN.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:
【题目】如图①,在梯形ABCD中,AD∥BC,∠A=60°,动点P从A点出发,以1cm/s的速度沿着A→B→C→D的方向不停移动,直到点P到达点D后才停止.已知△PAD的面积S(单位:cm2)与点P移动的时间(单位:s)的函数如图②所示,则点P从开始移动到停止移动一共用了秒(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线l1∥l2∥l3 , 且l1与l2的距离为1,l2与l3的距离为3,把一块含有45°角的直角三角形如图放置,顶点A,B,C恰好分别落在三条直线上,AC与直线l2交于点D,则线段BD的长度为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解学生参加家务劳动的情况,某中学随机抽取部分学生,统计他们双休日两天家务劳动的时间,将统计的劳动时间(单位:分钟)分成5组:30≤x<60,60≤x<90,90≤x<120,120≤x<150,150≤x<180,绘制成频数分布直方图.请根据图中提供的信息,解答下列问题:
(1)这次抽样调查的样本容量是;
(2)根据小组60≤x<90的组中值75,估计该组中所有数据的和为;
(3)该中学共有1000名学生,估计双休日两天有多少名学生家务劳动的时间不小于90分钟? 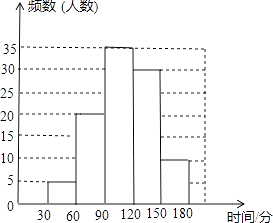
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图△ABC中,AB=AC=10厘米,BC=12厘米,D是BC的中点,点P从B出发,以a厘米/秒(a>0)的速度沿BA匀速向点A运动,点Q同时以1厘米/秒的速度从D出发,沿DB匀速向点B运动,其中一个动点到达端点时,另一个动点也随之停止运动,设它们运动的时间为t秒.
(1)若a=2,△BPQ∽△BDA,求t的值;
(2)设点M在AC上,四边形PQCM为平行四边形. ①若a= ![]() ,求PQ的长;
,求PQ的长;
②是否存在实数a,使得点P在∠ACB的平分线上?若存在,请求出a的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第十六届亚远会共颁发金牌477枚,如图是不完整的金牌数条形统计图和扇形统计图, 

根据以上信息.觯答下列问题:
(1)请将条形统计图补充完整;
(2)中国体育健儿在第十六届亚运会上共夺得金牌枚;
(3)在扇形统计图中,日本代表团所对应的扇形的圆心角约为°(精确到1°).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com