
【题目】直线l1∥l2∥l3 , 且l1与l2的距离为1,l2与l3的距离为3,把一块含有45°角的直角三角形如图放置,顶点A,B,C恰好分别落在三条直线上,AC与直线l2交于点D,则线段BD的长度为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
【答案】A
【解析】解:分别过点A、B、D作AF⊥l3 , BE⊥l3 , DG⊥l3 , 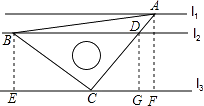
∵△ABC是等腰直角三角形,
∴AC=BC,
∵∠EBC+∠BCE=90°,∠BCE+∠ACF=90°,∠ACF+∠CAF=90°,
∴∠EBC=∠ACF,∠BCE=∠CAF,
在△BCE与△ACF中,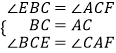 ,
,
∴△BCE≌△ACF(ASA)
∴CF=BE,CE=AF,
∵l1与l2的距离为1,l2与l3的距离为3,
∴CF=BE=3,CE=AF=3+1=4,
在Rt△ACF中,
∵AF=4,CF=3,
∴AC= ![]() =
= ![]() =5,
=5,
∵AF⊥l3 , DG⊥l3 ,
∴△CDG∽△CAF,
∴ ![]() ,
, ![]() =
= ![]() ,解得CD=
,解得CD= ![]() ,
,
在Rt△BCD中,
∵CD= ![]() ,BC=5,
,BC=5,
∴BD= ![]() =
= ![]() =
= ![]() .
.
故选A.
【考点精析】利用等腰直角三角形和平行线之间的距离对题目进行判断即可得到答案,需要熟知等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;两条平行线的距离:两条直线平行,从一条直线上的任意一点向另一条直线引垂线,垂线段的长度,叫做两条平行线的距离.


科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过△ABC的三个顶点,与y轴相交于(0, ![]() ),点A坐标为(﹣1,2),点B是点A关于y轴的对称点,点C在x轴的正半轴上.
),点A坐标为(﹣1,2),点B是点A关于y轴的对称点,点C在x轴的正半轴上. 
(1)求该抛物线的函数关系表达式.
(2)点F为线段AC上一动点,过F作FE⊥x轴,FG⊥y轴,垂足分别为E、G,当四边形OEFG为正方形时,求出F点的坐标.
(3)将(2)中的正方形OEFG沿OC向右平移,记平移中的正方形OEFG为正方形DEFG,当点E和点C重合时停止运动,设平移的距离为t,正方形的边EF与AC交于点M,DG所在的直线与AC交于点N,连接DM,是否存在这样的t,使△DMN是等腰三角形?若存在,求t的值;若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】轮船沿江从A港顺流行驶到B港,比从B港返回A港少用2小时,若船速为26千米/时,水速为3千米/时,求A港和B港相距多少千米.设A港和B港相距x千米.根据题意,可列出的方程是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘核潜艇在海面DF下600米A点处测得俯角为30°正前方的海底C点处有黑匣子,继续在同一深度直线航行1464米到B点处测得正前方C点处的俯角为45°.求海底C点处距离海面DF的深度(结果精确到个位,参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732,
≈1.732, ![]() ≈2.236)
≈2.236)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在3×3的方格纸中,点A、B、C、D、E、F分别位于如图所示的小正方形的顶点上. 
(1)从A、D、E、F四个点中任意取一点,以所取的这一点及点B、C为顶点画三角形,则所画三角形是等腰三角形的概率是;
(2)从A、D、E、F四个点中先后任意取两个不同的点,以所取的这两点及点B、C为顶点画四边形,求所画四边形是平行四边形的概率是(用树状图或列表法求解).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数的图象与x轴相交于点A(﹣3,0)、B(﹣1,0),与y轴相交于点C(0,3),点P是该图象上的动点;一次函数y=kx﹣4k(k≠0)的图象过点P交x轴于点Q.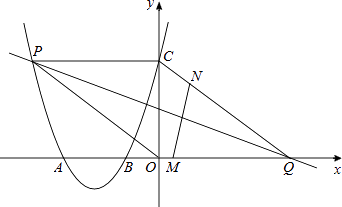
(1)求该二次函数的解析式;
(2)当点P的坐标为(﹣4,m)时,求证:∠OPC=∠AQC;
(3)点M,N分别在线段AQ、CQ上,点M以每秒3个单位长度的速度从点A向点Q运动,同时,点N以每秒1个单位长度的速度从点C向点Q运动,当点M,N中有一点到达Q点时,两点同时停止运动,设运动时间为t秒.
①连接AN,当△AMN的面积最大时,求t的值;
②直线PQ能否垂直平分线段MN?若能,请求出此时点P的坐标;若不能,请说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某测量船位于海岛P的北偏西60°方向,距离海岛100海里的A处,它沿正南方向航行一段时间后,到达位于海岛P的西南方向上的B处,求测量船从A处航行到B处的路程(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某玩具由一个圆形区域和一个扇形区域组成,如图,在⊙O1和扇形O2CD中,⊙O1与O2C、O2D分别切于点A、B,已知∠CO2D=60°,E、F是直线O1O2与⊙O1、扇形O2CD的两个交点,且EF=24cm,设⊙O1的半径为xcm. 
(1)用含x的代数式表示扇形O2CD的半径;
(2)若⊙O1和扇形O2CD两个区域的制作成本分别为0.45元/cm2和0.06元/cm2 , 当⊙O1的半径为多少时,该玩具的制作成本最小?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了进一步推进海南国际旅游岛建设,海口市自2012年4月1日起实施《海口市奖励旅行社开发客源市场暂行办法》,第八条规定:“旅行社引进会议规模达到200人以上,入住本市A类旅游饭店,每次会议奖励2万元;入住本市B类旅游饭店,每次会议奖励1万元.”某旅行社5月份引进符合奖励规定的会议共18次,得到28万元奖金,求此旅行社引进符合奖励规定的入住A类和B类旅游饭店的会议各多少次?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com