
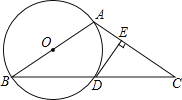
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC于点E.
(1)求证:DE是⊙O的切线.
(2)若∠B=30°,AB=8,求DE的长.
 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
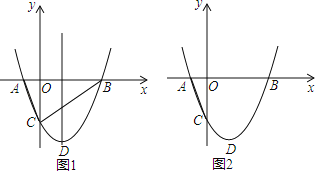
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是抛物线对称轴上的一个动点,当CM+AM的值最小时,求M的坐标;
(4)在线段BC下方的抛物线上有一动点P,求△PBC面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一批电视机,一月份每台毛利润是售出价的20%(毛利润=售出价-买入价),二月份该商场将每台售出价调低10%(买入价不变),结果销售台数比一月份增加120%,那么二月份的毛利润总额与一月份毛利润总额的比是__________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为6的正方形,点E在边AB上,BE=4,过点E作EF∥BC,分别交BD、CD于G、F两点.若M、N分别是DG、CE的中点,则MN的长为 ( )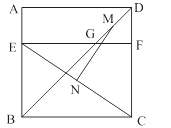
A.3
B.![]()
C.![]()
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A(-5,0),B(-3,0),点C在y轴的正半轴上,∠CBO=45°,CD∥AB.∠CDA=90°.点P从点Q(4,0)出发,沿x轴向左以每秒1个单位长度的速度运动,运动时时间t秒.
(1)求点C的坐标;
(2)当∠BCP=15°时,求t的值;
(3)以点P为圆心,PC为半径的⊙P随点P的运动而变化,当⊙P与四边形ABCD的边(或边所在的直线)相切时,求t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com