
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 先把a当常数解分式方程,x=$\frac{a+3}{a-1}$,再将a当常数解不等式组,根据不等式组无解得:a≤6,找出当a为非负整数时,x也是整数的值时,a有几个即可.
解答 解:$\frac{ax}{x-2}$=$\frac{3+a}{x-2}$-$\frac{x}{2-x}$,
去分母,方程两边同时乘以x-2,
ax=3+a+x,
x=$\frac{a+3}{a-1}$,且x≠2,
$\left\{\begin{array}{l}{2x-3>9①}\\{x-a<0②}\end{array}\right.$,
由①得:x>6,
由②得:x<a,
∵不等式组$\left\{\begin{array}{l}{2x-3>9}\\{x-a<0}\end{array}\right.$无解,
∴a≤6,
当a=0时,x=$\frac{a+3}{a-1}$=-3,
当a=1时,x=$\frac{a+3}{a-1}$无意义,
当a=2时,x=$\frac{a+3}{a-1}$=$\frac{2+3}{2-1}$=5,
当a=3时,x=$\frac{a+3}{a-1}$=$\frac{3+3}{3-1}$=3,
当a=4时,x=$\frac{a+3}{a-1}$=$\frac{4+3}{4-1}$=$\frac{7}{3}$,
当a=5时,x=$\frac{a+3}{a-1}$=$\frac{5+3}{5-1}$=2,分式方程无解,不符合题意,
当a=6时,x=$\frac{a+3}{a-1}$=$\frac{6+3}{6-1}$=$\frac{9}{5}$,
∵x是整数,a是非负整数,
∴a=0,2,3;
故选B.
点评 此题考查了解分式方程、一元一次不等式组的解的情况,求出分式方程和不等式组的解是解本题的关键,要注意分式方程有意义,即分母不为0.


 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:填空题
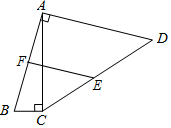 如图,四边形ABCD中,AB=AD,∠ACB=∠BAD=90°,E、F分别为CD、AB的中点,BC=2,CD=2$\sqrt{13}$,则EF=$\sqrt{17}$.
如图,四边形ABCD中,AB=AD,∠ACB=∠BAD=90°,E、F分别为CD、AB的中点,BC=2,CD=2$\sqrt{13}$,则EF=$\sqrt{17}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
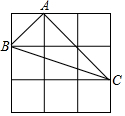 如图的3×3的正方形网格中,△ABC的顶点都在小正方形的格点上,这样的三角形称为格点三角形,在网格中与△ABC关于某直线成轴对称的格点三角形共有m个,则m=5.
如图的3×3的正方形网格中,△ABC的顶点都在小正方形的格点上,这样的三角形称为格点三角形,在网格中与△ABC关于某直线成轴对称的格点三角形共有m个,则m=5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
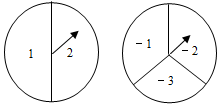 如图,有A、B两个转盘,A转盘被二等分,分别标有数字1和2.B转盘被三等分,分别标有数字-1,-2和-3.小强分别转动A盘、B盘各一次(若指针恰好指在分割线上,则重转一次,直到指针指向一个数字为止).记录A盘指针所对区域的数字为a,B盘指针所对区域的数字为b,这样就确定点Q的一个坐标为(a,b).
如图,有A、B两个转盘,A转盘被二等分,分别标有数字1和2.B转盘被三等分,分别标有数字-1,-2和-3.小强分别转动A盘、B盘各一次(若指针恰好指在分割线上,则重转一次,直到指针指向一个数字为止).记录A盘指针所对区域的数字为a,B盘指针所对区域的数字为b,这样就确定点Q的一个坐标为(a,b).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
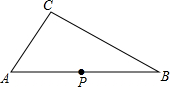 如图,点P是三角形ABC的边AB上一点,
如图,点P是三角形ABC的边AB上一点,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com