
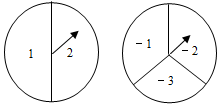 ��ͼ����A��B����ת�̣�Aת�̱����ȷ֣��ֱ��������1��2��Bת�̱����ȷ֣��ֱ��������-1��-2��-3��Сǿ�ֱ�ת��A�̡�B�̸�һ�Σ���ָ��ǡ��ָ�ڷָ����ϣ�����תһ�Σ�ֱ��ָ��ָ��һ������Ϊֹ������¼A��ָ���������������Ϊa��B��ָ���������������Ϊb��������ȷ����Q��һ������Ϊ��a��b����
��ͼ����A��B����ת�̣�Aת�̱����ȷ֣��ֱ��������1��2��Bת�̱����ȷ֣��ֱ��������-1��-2��-3��Сǿ�ֱ�ת��A�̡�B�̸�һ�Σ���ָ��ǡ��ָ�ڷָ����ϣ�����תһ�Σ�ֱ��ָ��ָ��һ������Ϊֹ������¼A��ָ���������������Ϊa��B��ָ���������������Ϊb��������ȷ����Q��һ������Ϊ��a��b�������� ��1��������״ͼ�����ɽ�����⣮
��2���жϳ���Q����ֱ��y=x-3�ϵĿ������Σ�������ʼ��ɣ�
��� �⣺��1����״ͼ��ͼ��ʾ��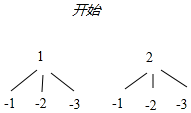
��Q�����п���������6�֣���1��-1������1��-2������1��-3������2��-1������2��-2������2��-3����
��2����Q����ֱ��y=x-3�ϵ��У�1��-2������2��-1���������Σ�
���Q����ֱ��y=x-3�ϵĸ���=$\frac{2}{6}$=$\frac{1}{3}$��
���� ���⿼���б�������״ͼ��һ�κ�����֪ʶ������Ĺؼ���ѧ������״ͼ���б�������������⣬���ڻ����⣬�п��������ͣ�


 ÿ��10���ӿ�����������������ϵ�д�
ÿ��10���ӿ�����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2�� | B�� | 3�� | C�� | 4�� | D�� | 5�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com