
分析 (1)设该市原来每立方米水价是x元,则现在每立方米水价是$\frac{4}{3}$x元,根据数量=总价÷单价结合该校今年1月份的用水量比去年11月份的用水量多600m3,即可得出关于x的分式方程,解之经检验后即可得出结论;
(2)用1月份的费用×(1-20%)即可求出该校今年5月份应交的水费.
解答 解:(1)设该市原来每立方米水价是x元,则现在每立方米水价是$\frac{4}{3}$x元,
根据题意得:$\frac{3600}{\frac{4}{3}x}$-$\frac{1800}{x}$=600,
解得:x=1.5,
经检验,x=1.5是方程$\frac{3600}{\frac{4}{3}x}$-$\frac{1800}{x}$=600的解.
(2)3600×(1-20%)=2880(元).
答:该校今年5月份应交的水费是2880元.
点评 本题考查了分式方程的应用,解题的关键是:(1)根据数量=总价÷单价列出关于x的分式方程;(2)根据数量关系列式计算.


科目:初中数学 来源: 题型:填空题
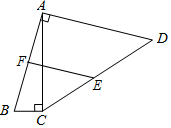 如图,四边形ABCD中,AB=AD,∠ACB=∠BAD=90°,E、F分别为CD、AB的中点,BC=2,CD=2$\sqrt{13}$,则EF=$\sqrt{17}$.
如图,四边形ABCD中,AB=AD,∠ACB=∠BAD=90°,E、F分别为CD、AB的中点,BC=2,CD=2$\sqrt{13}$,则EF=$\sqrt{17}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
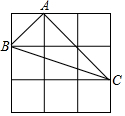 如图的3×3的正方形网格中,△ABC的顶点都在小正方形的格点上,这样的三角形称为格点三角形,在网格中与△ABC关于某直线成轴对称的格点三角形共有m个,则m=5.
如图的3×3的正方形网格中,△ABC的顶点都在小正方形的格点上,这样的三角形称为格点三角形,在网格中与△ABC关于某直线成轴对称的格点三角形共有m个,则m=5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
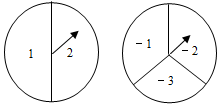 如图,有A、B两个转盘,A转盘被二等分,分别标有数字1和2.B转盘被三等分,分别标有数字-1,-2和-3.小强分别转动A盘、B盘各一次(若指针恰好指在分割线上,则重转一次,直到指针指向一个数字为止).记录A盘指针所对区域的数字为a,B盘指针所对区域的数字为b,这样就确定点Q的一个坐标为(a,b).
如图,有A、B两个转盘,A转盘被二等分,分别标有数字1和2.B转盘被三等分,分别标有数字-1,-2和-3.小强分别转动A盘、B盘各一次(若指针恰好指在分割线上,则重转一次,直到指针指向一个数字为止).记录A盘指针所对区域的数字为a,B盘指针所对区域的数字为b,这样就确定点Q的一个坐标为(a,b).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com