
【题目】如图,△ABC,∠ABC、∠ACB的三等分线交于点E、D,若∠BFC=132°,∠BGC=120°,则∠E的度数为( ) 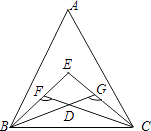
A.102°
B.104°
C.106°
D.108°
【答案】D
【解析】解:∵∠ABC、∠ACB的三等分线交于点E、D, ∴∠FBC=2∠DBC,∠GCB=2∠DCB,
∵∠BFC=132°,∠BGC=120°,
∴∠FBC+∠DCB=180°﹣∠BFC=180°﹣132°=48°,
∠DBC+∠GCB=180°﹣∠BGC=180°﹣120°=60°,
即 ![]() ,
,
由①+②可得:3(∠DBC+∠DCB)=108°,
∴∠EBC+∠ECB=2(∠DBC+∠DCB)=72°,
∴∠E=180°﹣(∠EBC+∠ECB)=180°﹣72°=108°,
故选D.
由三角形内角和及角平分线的定义可得到关于∠DBC和∠DCB的方程组,可求得∠DBC+∠DCB,则可求得∠EBC+∠ECB,再利用三角形内角和可求得∠E的度数.


科目:初中数学 来源: 题型:
【题目】已知两个变量x和y,它们之间的3组对应值如下表所示:
x | -1 | 0 | 1 |
y | -1 | 1 | 3 |
则y与x之间的函数关系式可能是( )
A. y=x B. y=2x+1 C. y=x2+x+1 D. y=3x
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°,CD⊥AB,AC=2,BC=3,若以C为圆心,以2为半径做⊙C,则点A在⊙C______,点B在⊙C________,点D在⊙C________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一个长为4a、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图2). 
(1)图2中的阴影部分的面积为;
(2)观察图2请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是;
(3)根据(2)中的结论,若x+y=7,xy= ![]() ,则x﹣y=;
,则x﹣y=;
(4)实际上通过计算图形的面积可以探求相应的等式.根据图3,写出一个因式分解的等式 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果a=(﹣ ![]() )2、b=(﹣2014)0、c=(﹣
)2、b=(﹣2014)0、c=(﹣ ![]() )﹣1 , 那么a、b、c的大小关系为( )
)﹣1 , 那么a、b、c的大小关系为( )
A.a>b>c
B.a>c>b
C.c>b>a
D.c>a>b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在第1个△A1BC中,∠B=30°,A1B=CB;在边A1B上任取一点D,延长CA1到A2 , 使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3 , 使A2A3=A2E,得到第3个△A2A3E,…按此做法继续下去,则第n个三角形中以An为顶点的内角度数是 . 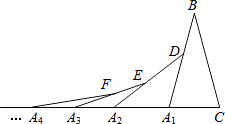
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,线段A′B′是由线段AB经过平移得到的,已知点A(﹣2,1)的对应点为A′(3,1),点B的对应点为B′(4,0),则点B的坐标为( )
A.(9,0)
B.(﹣1,0)
C.(3,﹣1)
D.(﹣3,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作题 画图并填空.
(1)已知△ABC中,∠ACB=90°,AC=3个单位,BC=4个单位.画出把△ABC 沿射线BC方向平移2个单位后得到△DEF;直接写出△DCF的面积为 .
(2)小明有一张边长为13cm的正方形纸片(如图1),他想将其剪拼成一块一边为8cm,的长方形纸片.他想了一下,不一会儿就把原来的正方形纸片剪拼成了一张宽8cm,长21cm的长方形纸片(如图2),你认为小明剪拼得对吗?请说明理由. 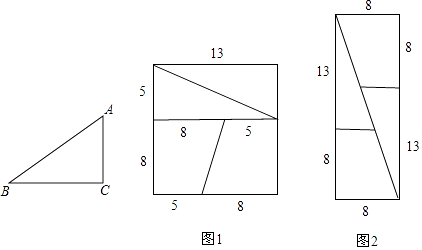
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com