
����Ŀ����ͼ1��һ����Ϊ4a����Ϊb�ij����Σ���ͼ�������ü���ƽ���ֳ��Ŀ�С�����Σ�Ȼ�����Ŀ�С������ƴ�ɵ�һ�������Ρ������Σ���ͼ2���� 
��1��ͼ2�е���Ӱ���ֵ����Ϊ��
��2���۲�ͼ2����д����a+b��2����a��b��2��ab֮��ĵ�����ϵ����
��3�����ݣ�2���еĽ��ۣ���x+y=7��xy= ![]() ����x��y=��
����x��y=��
��4��ʵ����ͨ������ͼ�ε��������̽����Ӧ�ĵ�ʽ������ͼ3��д��һ����ʽ�ֽ�ĵ�ʽ ��
���𰸡�
��1����b��a��2
��2����a+b��2����a��b��2=4ab
��3����2
��4��3a2+4ab+b2=��a+b��?��3a+b��
���������⣺��1����Ӱ����Ϊ�߳�Ϊ��b��a���������Σ�������Ӱ���ֵ������b��a��2 �� �ʴ�Ϊ����b��a��2����2��ͼ2�У��ñ߳�Ϊa+b�������ε������ȥ�߳�Ϊb��a�������ε���4�������ֱ�a��b�ľ��������
���ԣ�a+b��2����a��b��2=4ab��
�ʴ�Ϊ����a+b��2����a��b��2=4ab�� ��3���ߣ�x+y��2����x��y��2=4xy��
��x+y=7��xy= ![]() ��
��
��72����x��y��2=4�� ![]() ��
��
�ࣨx��y��2=4��
��x��y=��2��
�ʴ�Ϊ����2����4���߳�Ϊ��a+b���루3a+b���ľ������Ϊ��a+b����3a+b��������3���߳�Ϊa�������Ρ�4���߳�Ϊa��b�ľ��κ�һ���߳�Ϊb����������ɣ�
��3a2+4ab+b2=��a+b����3a+b����
�ʴ�Ϊ��3a2+4ab+b2=��a+b����3a+b����
��1����Ӱ����Ϊ�߳�Ϊ��b��a���������Σ�Ȼ����������ε������ʽ��⣻��2����ͼ2�У�����������С�����κ�4��������ɣ���a+b��2����a��b��2=4ab�� ��3���ɣ�2���Ľ��۵õ���x+y��2����x��y��2=4xy���ٰ�x+y=7��xy= ![]() �õ���x��y��2=4��Ȼ������ƽ�����Ķ�����⣻��4���۲�ͼ�εõ��߳�Ϊ��a+b���루3a+b���ľ�����3���߳�Ϊa�������Ρ�4���߳�Ϊa��b�ľ��κ�һ���߳�Ϊb����������ɣ�����3a2+4ab+b2=��a+b����3a+b����
�õ���x��y��2=4��Ȼ������ƽ�����Ķ�����⣻��4���۲�ͼ�εõ��߳�Ϊ��a+b���루3a+b���ľ�����3���߳�Ϊa�������Ρ�4���߳�Ϊa��b�ľ��κ�һ���߳�Ϊb����������ɣ�����3a2+4ab+b2=��a+b����3a+b����


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ����ǿ����������ʶ��6��5�ա����绷���ա����죬�ڻ����ֹ�����Աָ���£�������������С��ʿ����ɵġ�����������Ⱦ������ѧϰ�о�С�飬����������ȫ��40��������������ijʱ�̵�������������λ��dB��������������ݽ��д����������������������������ò�����Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ���£�
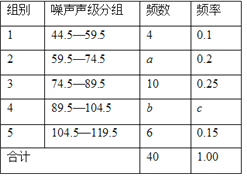
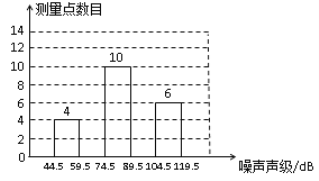
���ݱ����ṩ����Ϣ����������⣺
��1��Ƶ���ֲ����е�a =________��b=________��c =_________��
��2���벹ȫƵ���ֲ�ֱ��ͼ��
��3�����ȫ�й���200�������㣬��ô����һʱ����������С��75dB�IJ�����Լ�ж��ٸ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����x����2�������в���ʽ��������(����)
A. x2����2x B. x2�ݣ�2x C. x2����2x D. x2�ܣ�2x
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������⣺
��1��30������3��2���� ![]() ����1
����1
��2������3x��3+��x4��2�£���x��5
��3����a+b��2����a��b+2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ü������������и�ֵ������ȷ��0.001��
��1��sin20�㣻
��2��cos63��35�䣻
��3��sin87��17��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�ı���ABCD�У��Խ���BDƽ�֡�ABC����ACB=72�㣬��ABC=50�㣬���ҡ�BAD+��CAD=180�㣬��ô��ADC�Ķ���Ϊ�� �� 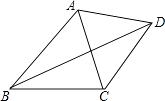
A.62��
B.65��
C.68��
D.70��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC����ABC����ACB�����ȷ��߽��ڵ�E��D������BFC=132�㣬��BGC=120�㣬���E�Ķ���Ϊ�� �� 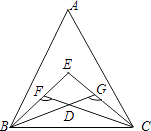
A.102��
B.104��
C.106��
D.108��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A�ڵڶ�������������Ϊ1����B��x��ĸ������ϣ�AB=AO����ABO=30�㣬ֱ��MN����ԭ��O����A����ֱ��MN�ĶԳƵ�A1��x����������ϣ���B����ֱ��MN�ĶԳƵ�ΪB1 �� 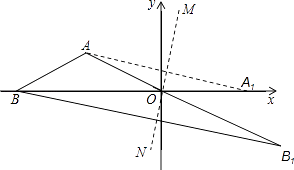
��1�����AOM�Ķ�����
��2����֪30�㣬60�㣬90������������߱�Ϊ1�� ![]() ��2�����߶�AB1�ij���B1�������꣮
��2�����߶�AB1�ij���B1�������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����x��3����y�ĺͲ�С��2���ò���ʽ�ɱ�ʾΪ(�� ��)
A. 3x��y��2 B. 3(x��y)��2 C. 3x��y��2 D. 3(x��y)��2
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com