
【题目】如图,在平面直角坐标系中,点A在第二象限且纵坐标为1,点B在x轴的负半轴上,AB=AO,∠ABO=30°,直线MN经过原点O,点A关于直线MN的对称点A1在x轴的正半轴上,点B关于直线MN的对称点为B1 . 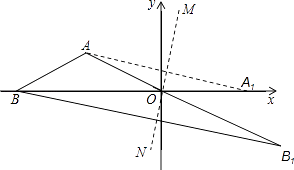
(1)求∠AOM的度数.
(2)已知30°,60°,90°的三角形三边比为1: ![]() :2,求线段AB1的长和B1的纵坐标.
:2,求线段AB1的长和B1的纵坐标.
【答案】
(1)
解:∵点A与点A1关于直线MN对称,
∴∠AOM=∠A1OM,
∵AB=AO,∠ABO=30°,
∴∠AOB=30°,
∵∠AOB+∠AOM+∠A1OM=180°,
∴∠AOM=75°
(2)
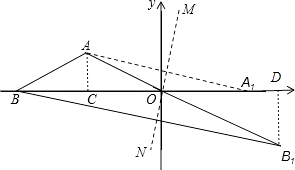
解:过点A作AC⊥x轴于点C,过点B1作B1D⊥x轴于点D,如图所示.
∵∠AOC=30°,∠ACO=90°,AC=1,
∴AO=2AC=2,OC= ![]() AC=
AC= ![]() ,
,
∵AB=AO,
∴BO=2OC=2 ![]() ,
,
∴点A(﹣ ![]() ,1),点B(﹣2
,1),点B(﹣2 ![]() ,0).
,0).
∵点A与点A1关于直线MN对称,
∴OA1=OA=2,
∴点A1(2,0),
∴A1B=2﹣(﹣2 ![]() )=2+2
)=2+2 ![]() ,
,
∵点A关于直线MN的对称点A1,点B关于直线MN的对称点为B1,
∴AB1=A1B=2+2 ![]() ,OB1=OB=2
,OB1=OB=2 ![]() .
.
在Rt△OB1D中,∠B1OD=∠AOB=30°,
∴B1D= ![]() OB1=
OB1= ![]() .
.
故线段AB1的长为2+2 ![]() ,B1的纵坐标为
,B1的纵坐标为 ![]() .
.
【解析】(1)由点A与点A1关于直线MN对称,可得出∠AOM=∠A1OM,再由等腰三角形的性质可得出∠AOB=30°,通过角的计算即可得出结论;(2)过点A作AC⊥x轴于点C,过点B1作B1D⊥x轴于点D,通过解直角三角形以及等腰三角形的性质可得出点A、B点的坐标,再根据对称的性质即可得出点A1的坐标以及AB1=A1B,在Rt△OB1D中,利用特殊角的三角函数值即可得出B1D的长度,此题得解.
【考点精析】本题主要考查了三角形三边关系和比例的性质的相关知识点,需要掌握三角形两边之和大于第三边;三角形两边之差小于第三边;不符合定理的三条线段,不能组成三角形的三边;基本性质;更比性质(交换比例的内项或外项);反比性质(交换比的前项、后项);等比性质才能正确解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】完成以下任务,适合用抽样调查的是( )
A. 调查你班同学的年龄情况 B. 考察一批炮弹的杀伤半径
C. 为订购校服,了解学生衣服的尺寸 D. 对航天飞机上的零部件进行检查
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一个长为4a、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图2). 
(1)图2中的阴影部分的面积为;
(2)观察图2请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是;
(3)根据(2)中的结论,若x+y=7,xy= ![]() ,则x﹣y=;
,则x﹣y=;
(4)实际上通过计算图形的面积可以探求相应的等式.根据图3,写出一个因式分解的等式 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在第1个△A1BC中,∠B=30°,A1B=CB;在边A1B上任取一点D,延长CA1到A2 , 使A1A2=A1D,得到第2个△A1A2D;在边A2D上任取一点E,延长A1A2到A3 , 使A2A3=A2E,得到第3个△A2A3E,…按此做法继续下去,则第n个三角形中以An为顶点的内角度数是 . 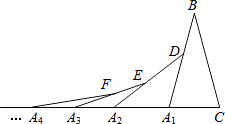
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,线段A′B′是由线段AB经过平移得到的,已知点A(﹣2,1)的对应点为A′(3,1),点B的对应点为B′(4,0),则点B的坐标为( )
A.(9,0)
B.(﹣1,0)
C.(3,﹣1)
D.(﹣3,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作题 画图并填空.
(1)已知△ABC中,∠ACB=90°,AC=3个单位,BC=4个单位.画出把△ABC 沿射线BC方向平移2个单位后得到△DEF;直接写出△DCF的面积为 .
(2)小明有一张边长为13cm的正方形纸片(如图1),他想将其剪拼成一块一边为8cm,的长方形纸片.他想了一下,不一会儿就把原来的正方形纸片剪拼成了一张宽8cm,长21cm的长方形纸片(如图2),你认为小明剪拼得对吗?请说明理由. 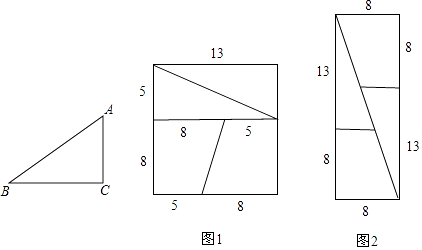
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在五边形ABCDE中,∠A+∠B+∠E=α,DP、CP分别平分∠EDC、∠BCD,则∠P的度数是( ) 
A.![]() α﹣90°
α﹣90°
B.90° ![]()
C.![]()
D.540° ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com