
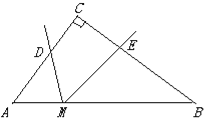
【题目】如图,在Rt△ABC中,已知AC=3,BC=4,点M是AB边上的一个动点,∠DME的两边与折线A—C—B分别交于点D和点E(点E在点D的右边),且∠DME=∠A,若能使以点D,E,M为顶点的三角形与△ABC相似的点D有三个,则AM的长度x的取值范围是________.
【答案】![]() 或
或![]()
【解析】
当CM⊥AB于点M,DM⊥AC于点D时,此时点C,E重合,根据已知条件易证△DCM∽△CAB∽△ACM,利用相似三角形的对应边成比例,可求出x的值,即可得到x的取值范围;如图,当点M为AB的中点,ME⊥BC于点E,点C、D重合,利用直角三角形斜边的性质,可求出AM的长,同理可得到点D的另一个点,综上所述,可得到x的取值范围.
如图,CM⊥AB于点M,DM⊥AC于点D,此时点C,E重合,
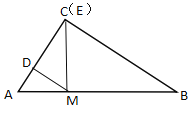
∴∠CDM=∠ACB=∠AMC=90°,
∴∠DMC+∠ADM=90°,∠ADM+∠A=90°,
∴∠A=∠DME
∴△DCM∽△CAB∽△ACM,
∴![]()
在Rt△ABC中,
![]()
∴![]()
解得![]() ,
,
∴0<x<![]() ;
;
如图,当点M为AB的中点,ME⊥BC于点E,点C、D重合.
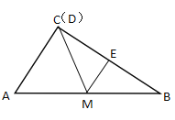
∵BC⊥AC
∴ME∥AC
∴∠CME=∠ACM
∵CM是Rt△ABC的中线,
∴CM=AM=BM=![]() ,
,
∴∠A=∠ACM=∠CME
∴x=![]() ;
;
同理可得到点D的另一个点,此时![]()
∴x的取值范围为 ![]() <x<
<x<![]()
故答案为:![]() 或
或![]()


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:
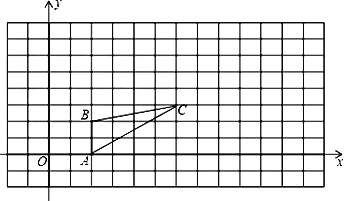
【题目】如图,图中的小方格都是边长为1的正方形,△ABC的A、B、C三点坐标为A(2,0)、B(2,2)、C(6,3)。
(1) 请在图中画出一个△![]() ,使△
,使△![]() 与△ABC是以坐标原点为位似中心,相似比为2的位似图形。
与△ABC是以坐标原点为位似中心,相似比为2的位似图形。
(2)求△![]() 的面积。
的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一张边长为10cm的正方形纸板的四周各剪去一个边长为xcm的小正方形,再折叠成一个无盖的长方体盒子.
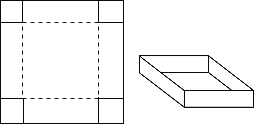
(1)当长方体盒子的底面积为81cm2时,求所剪去的小正方形的边长.
(2)设所折叠的长方体盒子的侧面积为S,求S与x的函数关系式,并写出x的取值范围.
(3)长方体盒子的侧面积为S的值能否是60cm2,若能,请求出x的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
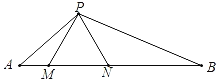
【题目】如图,在△PAB中,M.N是AB上两点,△PMN是等边三角形,∠APM=∠B.
(1)求证:∠A=∠BPN;
(2)求证:MN2=AM·BN;
(3)若AP=![]() ,AM=1,求线段MN,PB的长.
,AM=1,求线段MN,PB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
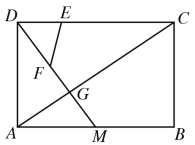
【题目】如图,在矩形ABCD中,AB=18,AD=12,点M是边AB的中点,连结DM,DM与AC交于点G,点E,F分别是CD与DG上的点,连结EF,
(1)求证:CG=2AG.
(2)若DE=6,当以E,F,D为顶点的三角形与△CDG相似时,求EF的长.
(3)若点E从点D出发,以每秒2个单位的速度向点C运动,点F从点G出发,以每秒1个单位的速度向点D运动.当一个点到达,另一个随即停止运动.在整个运动过程中,求四边形CEFG的面积的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
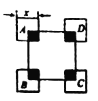
【题目】正方形ABCD的边长是10,四个全等的小正方形的对称中心分别在ABCD的顶点上,且它们的各边与正方形ABCD各边平行或垂直。若小正方形的边长为x,且![]() ,阴影部分的面积为y,则能反映y与x之间函数关系的大致图形是( )
,阴影部分的面积为y,则能反映y与x之间函数关系的大致图形是( )
A.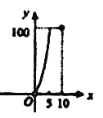 B.
B.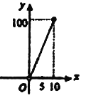 C.
C.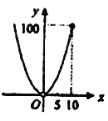 D.
D.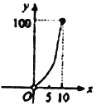
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】赣县田村素称“灯彩之乡”,田村花灯源于唐代,盛于宋朝,迄今已有1300多年历史了,某公司生产了一种田村花灯,每件田村花灯制造成本为20元.设销售单价x(元),每日销售量y(件)、每日的利润w(元).在试销过程中,每日销售量y(件)、每日的利润w(元)与销售单价x(元)之间存在一定的关系,其几组对应量如下表所示:
销售单价x(元) | 30 | 31 | 32 | 40 |
销售量y(件) | 40 | 38 | 36 | 20 |
(1)根据表中数据的规律、分別写出每日销售量y(件)、每日利润w(元)关于销售单价x(元)之间的函数表达式(利润=(销售单价﹣成本单价)×销售件数).
(2)当销售单价为多少元时,公司每日能够获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象分别交x轴、y轴于C,D两点,交反比例函数
的图象分别交x轴、y轴于C,D两点,交反比例函数![]() 图象于A(
图象于A(![]() ,4),B(3,m)两点.
,4),B(3,m)两点.
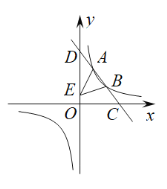
(1)求直线CD的表达式;
(2)点E是线段OD上一点,若![]() ,求E点的坐标;
,求E点的坐标;
(3)请你根据图象直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com