
【题目】如图,在平面直角坐标系xOy中,梯形AOBC的边OB在x轴的正半轴上,AC∥OB,BC⊥OB,过点A的双曲线![]() 的一支在第一象限交梯形对角线OC于点D,交边BC于点E.(1)填空:双曲线的另一支在第_____象限,k的取值范围是_____;
的一支在第一象限交梯形对角线OC于点D,交边BC于点E.(1)填空:双曲线的另一支在第_____象限,k的取值范围是_____;
(2)若点C的坐标为(2,2),当点E在什么位置时?阴影部分面积S最小?
(3)若![]() ,
, ![]() =2,求双曲线的解析式.
=2,求双曲线的解析式.

【答案】(1) 三,k>0 (2) 当点E在BC的中点时,阴影部分的面积S最小 (3) y=![]()
【解析】【试题分析】
(1)根据双曲线的性质,k>0,双曲线在一、三象限;k<0,在二、四象限.根据题意,该双曲线的另一支一定在第三象限,且k>0;
(2)由题意得:A点的纵坐标为2,E点的横坐标为2,根据反比例函数![]() ,设A点的坐标为(
,设A点的坐标为(![]() ,2),E点的坐标为(2,
,2),E点的坐标为(2, ![]() ),则阴影部分的面积为
),则阴影部分的面积为
S△ACE+S△OBE=![]() ×(2-
×(2-![]() )×(2-
)×(2-![]() )+
)+![]() ×2×
×2×![]() =
=![]()
![]() +
+![]() ,当k-2=0,即k=2时,
,当k-2=0,即k=2时, ![]() 最小,最小值为
最小,最小值为![]() ;即E点的坐标为(2,1),即E点为BC的中点.
;即E点的坐标为(2,1),即E点为BC的中点.
(3)设D点坐标为(a, ![]() ),根据中点坐标公式得C点坐标为(2a,
),根据中点坐标公式得C点坐标为(2a, ![]() ), 则A点的纵坐标为
), 则A点的纵坐标为![]() ,代入y=
,代入y=![]() 得,x=
得,x=![]() ,得A点坐标为(
,得A点坐标为(![]() ,
,![]() ),根据
),根据![]() =2,得
=2,得![]() ×(2a-
×(2a-![]() )×
)×![]() =2,解得k=
=2,解得k=![]() ,
,
【试题解析】
(1)三,k>0;
(2)∵梯形AOBC的边OB在x轴的正半轴上,AC∥OB,BC⊥OB,
而点C的坐标为(2,2),
∴A点的纵坐标为2,E点的横坐标为2,B点坐标为(2,0),把y=2代入y=![]() ,得,x=
,得,x=![]() ,
,
把x=2代入y=![]() 得,y=
得,y=![]() ,
,
∴A点的坐标为(![]() ,2),
,2),
E点的坐标为(2, ![]() ),
),
∴![]() =S△ACE+S△OBE,
=S△ACE+S△OBE,
=![]() ×(2-
×(2-![]() )×(2-
)×(2-![]() )+
)+![]() ×2×
×2×![]() ,
,
=![]()
![]() +
+![]() ,
,
当k-2=0,即k=2时, ![]() 最小,最小值为
最小,最小值为![]() ;
;
∴E点的坐标为(2,1),即E点为BC的中点,
∴当点E在BC的中点时,阴影部分的面积S最小;
(3)设D点坐标为(a, ![]() ),
),
∵![]() =
=![]() ,
,
∴2OD=OC,
即D点为OC的中点,
∴C点坐标为(2a, ![]() ),
),
∴A点的纵坐标为![]() ,
,
把y=![]() 代入y=
代入y=![]() 得,x=
得,x=![]() ,
,
∴A点坐标为(![]() ,
,![]() )
)
∵![]() =2,
=2,
∴![]() ×(2a-
×(2a-![]() )×
)×![]() =2,
=2,
∴k=![]() ,
,
∴双曲线的解析式为y=![]() .
.


科目:初中数学 来源: 题型:
【题目】下列去括号正确的是( )
A.a﹣2(﹣b+c)=a﹣2b﹣2c
B.a﹣2(﹣b+c)=a+2b﹣2c
C.a+2(b﹣c)=a+2b﹣c
D.a+2(b﹣c)=a+2b+2c
查看答案和解析>>
科目:初中数学 来源: 题型:
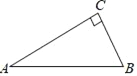
【题目】如图,在△ABC中,∠C=90°.
(1)用圆规和直尺在AC上作点P,使点P到A、B的距离相等.(保留作图痕迹,不写作法和证明)
(2)当满足(1)的点P到AB、BC的距离相等时,求∠A的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC
(2)若AB=4,AD=3![]() ,AE=3,求AF的长.
,AE=3,求AF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
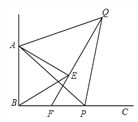
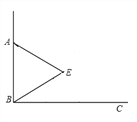
【题目】如图,已知∠ABC=90°,△ABE是等边三角形,点P为射线BC上任意一点(点P与点B不重合),连接AP,将线段AP绕点A逆时针旋转60°得到线段AQ,连接QE并延长交射线BC于点F.
(1)如图,当BP=BA时,∠EBF=______°,猜想∠QFC =______°;
(2)如图,当点P为射线BC上任意一点时,猜想∠QFC的度数,并加以证明.
(3)已知线段AB=![]() ,设BP=x,点Q到射线BC的距离为y,求y关于x的函数关系式.
,设BP=x,点Q到射线BC的距离为y,求y关于x的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() (其中
(其中![]() )与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,抛物线的对称轴l与x轴交于点D,且点D恰好在线段BC的垂直平分线上.
)与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,抛物线的对称轴l与x轴交于点D,且点D恰好在线段BC的垂直平分线上.
(1)求抛物线的关系式;
(2)过点![]() 的线段MN∥y轴,与BC交于点P,与抛物线交于点N.若点E是直线l上一点,且∠BED=∠MNB-∠ACO时,求点E的坐标.
的线段MN∥y轴,与BC交于点P,与抛物线交于点N.若点E是直线l上一点,且∠BED=∠MNB-∠ACO时,求点E的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(﹣1,0),对称轴为直线x=2,下列结论:
①4a+b=0;②9a+c>3b;③8a+7b+2c>0;④当x>﹣1时,y的值随x值的增大而增大;⑤当函数值y<0时,自变量x的取值范围是x<-1或x>5.
其中正确的结论有( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com