
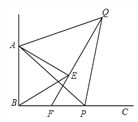
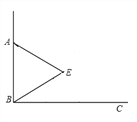
【题目】如图,已知∠ABC=90°,△ABE是等边三角形,点P为射线BC上任意一点(点P与点B不重合),连接AP,将线段AP绕点A逆时针旋转60°得到线段AQ,连接QE并延长交射线BC于点F.
(1)如图,当BP=BA时,∠EBF=______°,猜想∠QFC =______°;
(2)如图,当点P为射线BC上任意一点时,猜想∠QFC的度数,并加以证明.
(3)已知线段AB=![]() ,设BP=x,点Q到射线BC的距离为y,求y关于x的函数关系式.
,设BP=x,点Q到射线BC的距离为y,求y关于x的函数关系式.
【答案】(1)∠EBF=30°; ∠QFC=60°;(2)∠QFC=60°.(3)![]() (x>0).
(x>0).
【解析】试题分析:(1)∠EBF与∠ABE互余,而∠ABE=60°,即可求得∠EBF的度数;利用观察法,或量角器测量的方法即可求得∠QFC的度数;
(2)根据三角形的外角等于不相邻的两内角的和,证明∠BAP=∠EAQ,进而得到△ABP≌△AEQ,证得∠AEQ=∠ABP=90°,则∠BEF=180°-∠AEQ-∠AEB=180°-90°-60°=30°,∠QFC=∠EBF+∠BEF;
(3)过点F作FG⊥BE于点G,过点Q作QH⊥BC,根据△ABP≌△AEQ得到:设QE=BP=x,则QF=QE+EF=x+2.点Q到射线BC的距离y=QH=sin60°×QF=![]() (x+2),即可求得函数关系式.
(x+2),即可求得函数关系式.
试题解析:(1)∵∠ABC=90°,∠BAE=60°,
∴∠EBF=30°;
则猜想:∠QFC=60°;
(2)∠QFC=60°.
∵∠BAP=∠BAE+∠EAP=60°+∠EAP,∠EAQ=∠QAP+∠EAP=60°+∠EAP,
∴∠BAP=∠EAQ
在△ABP和△AEQ中,
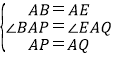 ,
,
∴△ABP≌△AEQ (SAS)
∴∠AEQ=∠ABP=90°
∴∠BEF=180°-∠AEQ-∠AEB=180°-90°-60°=30°,
∴∠QFC=∠EBF+∠BEF=30°+30°=60°;
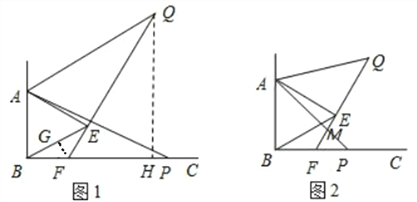
(3)在图1中,过点F作FG⊥BE于点G,过点Q作QH⊥BC于点H,
∵△ABE是等边三角形,
∴BE=AB=![]() ,
,
由(1)得∠EBF=30°,在Rt△BGF中,![]()
∴FG=2,BF=4,∴EF=BF=4,
∵△ABP≌△AEQ,∴QE=PB=x,∴QF=QE+EF=x+4,
由(2)得∠QFC=60°,∴在Rt△QHF中,∠FQH=30°
![]()
即y关于x的函数关系式是:![]() (x>0)
(x>0)
.


 步步高达标卷系列答案
步步高达标卷系列答案科目:初中数学 来源: 题型:
【题目】如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:
①2a+b=0;
②abc>0;
③方程ax2+bx+c=3有两个相等的实数根;
④抛物线与x轴的另一个交点是(-1,0);
⑤当1<x<4时,有y2<y1,

其中正确的是( ).
A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,梯形AOBC的边OB在x轴的正半轴上,AC∥OB,BC⊥OB,过点A的双曲线![]() 的一支在第一象限交梯形对角线OC于点D,交边BC于点E.(1)填空:双曲线的另一支在第_____象限,k的取值范围是_____;
的一支在第一象限交梯形对角线OC于点D,交边BC于点E.(1)填空:双曲线的另一支在第_____象限,k的取值范围是_____;
(2)若点C的坐标为(2,2),当点E在什么位置时?阴影部分面积S最小?
(3)若![]() ,
, ![]() =2,求双曲线的解析式.
=2,求双曲线的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两家绿化养护公司各自推出了校园绿化养护服务的收费方案.
甲公司方案:每月的养护费用y(元)与绿化面积x(平方米)是一次函数关系,如图所示.
乙公司方案:绿化面积不超过1000平方米时,每月收取费用5500元;绿化面积超过1000平方米时,每月在收取5500元的基础上,超过部分每平方米收取4元.

(1)求如图所示的y与x的函数解析式;(不要求写取值范围)
(2)如果某学校目前的绿化面积是1200平方米.试通过计算说明:选择哪家公司的服务,每月的绿化养护费用较少.
查看答案和解析>>
科目:初中数学 来源: 题型:
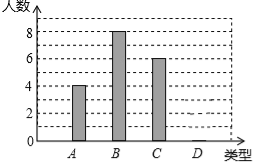
【题目】某校240名学生参加植树活动,要求每人植树4~7棵,活动结束后抽查了20名学生每人的植树量,并分为四类:A类4棵、B类5棵、C类6棵、D类7棵,将各类的人数绘制成如图所示不完整的条形统计图,回答下列问题:
(1)补全条形图;
(2)写出这20名学生每人植树量的众数和中位数;
(3)估计这240名学生共植树多少棵?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com