
����Ŀ���ס������˷ֱ������г���Ħ�г�����ͬһ�ص�����ͬ��·��ǰ������80km��ij�أ�ͼ��l1��l2�ֱ��ʾ�ס��������뿪�����صľ���s��km������ʻʱ��t��h��֮��ĺ�����ϵ�������ͼ�����������⣺
��1���ס�������˭����Ŀ�ĵؽ��磿��ʱ�䣿
��2���ֱ���ס���������ʻ������s��t�ĺ�����ϵʽ��
��3����ȷ����������������ʻ;�У������������غ�Ŀ�ĵأ�ʱ��t��ȡֵ��Χ��������һʱ����ڣ���tΪ��ֵʱ��Ħ�г���ʻ�����г�ǰ�棿

���𰸡���1���ҵ���Ŀ�ĵؽ��磬�ȼ���2Сʱ����2���ף�s��16t���ң� s��40t��40����3��1��x��3ʱ�����˾���ʻ��;�У������������յ㣩��![]() ʱ��Ħ�г���ʻ�����г�ǰ�森
ʱ��Ħ�г���ʻ�����г�ǰ�森
��������
��1�����ݺ���ͼ�����ֱ�ӽ���⣻
��2������ͼ���е����ݿ��Էֱ����l1��l2��Ӧ�ı���ʽ��
��3������ͼ��ɵõ�������������ʻ;�У������������غ�Ŀ�ĵأ�ʱ��t��ȡֵ��Χ�����ݣ�2���Ľ��������ֱ�ߵĽ������꼴�ɵó�tΪ��ֵʱ��Ħ�г���ʻ�����г�ǰ�森
�⣺��1������ͼ���֪���ҵ���Ŀ�ĵؽ��磬�ȼ���2Сʱ��
�ʴ�Ϊ���ҵ���Ŀ�ĵؽ��磬�ȼ���2Сʱ��
��2������ͼ���֪�����ٶ�Ϊ��80��5��16��km/h����
��l1��Ӧ�ı���ʽΪs��16t��
�ҵ��ٶ�Ϊ80����3��1����40��km/h����
��l2��Ӧ�ı���ʽΪs��40t+b���ѣ�3��80������ã�40��3+b��80�����b����40��
��l2��Ӧ�ı���ʽΪs��40t��40��
�ʴ�Ϊ���ף�s��16t���ң� s��40t��40��
��3����ͼ��ɵã�1��x��3ʱ�����˾���ʻ��;�У������������յ㣩��
����l1��l2��![]() �����
�����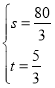 ��
��
��![]() ʱ��Ħ�г���ʻ�����г�ǰ�棬
ʱ��Ħ�г���ʻ�����г�ǰ�棬
�ʴ�Ϊ��1��x��3ʱ�����˾���ʻ��;�У������������յ㣩��![]() ʱ��Ħ�г���ʻ�����г�ǰ�森
ʱ��Ħ�г���ʻ�����г�ǰ�森


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�ı߳�Ϊ2��![]() ����EΪBC�ߵ��е㣬��PΪ�Խ���AC��һ���㣬��PB+PE����СֵΪ_____��
����EΪBC�ߵ��е㣬��PΪ�Խ���AC��һ���㣬��PB+PE����СֵΪ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
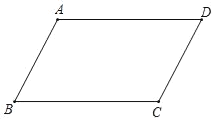
����Ŀ����ͼ���ı���ABCD��ƽ���ı��Σ�AE��BD�ڵ�E������EC��
(1)�����ⲹȫͼ�Σ�
(2)��ƽ������һ��F��ʹ���ı���ECFA��ƽ���ı��Σ�����ͼ�л�����F��������Ļ�ͼ���̣���֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������10�֣���ͼ����ֱ֪��![]() ��˫����
��˫����![]() ��k��0������A��m��n����˫����
��k��0������A��m��n����˫���� ![]() �ϣ���m=n=2ʱ��
�ϣ���m=n=2ʱ��
��1��ֱ��д��k��ֵ��
��2����ֱ��![]() ��������ƽ����ʹƽ�ƺ��ֱ����˫����
��������ƽ����ʹƽ�ƺ��ֱ����˫���� ![]() ֻ��һ��������
ֻ��һ��������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������������У�![]() ��
��![]() ��
��![]() ��Ϊ���(�����ָÿ��С�����εĶ���)����
��Ϊ���(�����ָÿ��С�����εĶ���)����![]() ����ƽ��6����λ�õ�
����ƽ��6����λ�õ�![]() .����������ֱ��ͼ��
.����������ֱ��ͼ��

��1�����������![]() ��
��
��2������![]() ���ϵ�����
���ϵ�����![]() ��
��![]() ���ϵĸ���
���ϵĸ���![]() ��
��
��3����![]() �ı�
�ı�![]() ��
��![]() �ֱ���
�ֱ���![]() �ı�
�ı�![]() ��
��![]() ��ֱ����
��ֱ����![]() �Ķ����� .
�Ķ����� .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��
��![]() �۵����
�۵����![]() ��
��![]() �غ�.��ԭ���εij���֮��Ϊ
�غ�.��ԭ���εij���֮��Ϊ![]() ,��
,��![]() ��ֵΪ�� ��
��ֵΪ�� ��

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��AB��CD �ཻ�ڵ�O����AOD=3��BOD+20��.
(1)���BOD�Ķ�����
(2)��OΪ�˵�������OE,OF ,����OEƽ�֡�BOD���ҡ�EOF= 90�������BOF�Ķ���.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����䷽�������з��̣�
��1��x2+2x-8=0 ��2��x2+12x-15=0
��3��x2-4x=16 ��4��x2=x+56
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���BAC=90����AD��BC����ABC��ƽ����BE��AD�ڵ�F��AGƽ�֡�DAC���������н��ۣ��١�BAD=��C���ڡ�AEF=��AFE���ۡ�EBC=��C����AG��EF����ȷ�����У�������

A. 4��B. 3��C. 2��D. 1��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com