
【题目】在菱形ABCD中,对角线AC、BD相交于点O,过点O作一条直线分别交DA、BC的延长线于点E、F,连接BE、DF. 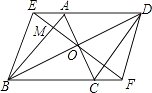
(1)求证:四边形BFDE是平行四边形;
(2)若EF⊥AB,垂足为M,tan∠MBO= ![]() ,求EM:MF的值.
,求EM:MF的值.
【答案】
(1)证明:在菱形ABCD中,AD∥BC,OA=OC,OB=OD,
∴∠AEO=∠CFO,
在△AEO和△CFO中,
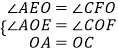 ,
,
∴△AEO≌△CFO(AAS),
∴OE=OF,
又∵OB=OD,
∴四边形BFDE是平行四边形
(2)解:设OM=2x,
∵EF⊥AB,tan∠MBO= ![]() ,
,
∴BM=3x,
又∵AC⊥BD,
∴∠AOM=∠OBM,
∴△AOM∽△OBM,
∴ ![]() =
= ![]() ,
,
∴AM= ![]() =
= ![]() x,
x,
∵AD∥BC,
∴△AEM∽△BFM,
∴EM:FM=AM:BM= ![]() x:3x=4:9.
x:3x=4:9.
【解析】(1)根据两直线平行,内错角相等可得∠AEO=∠CFO,然后利用“角角边”证明△AEO和△CFO全等,根据全等三角形对应边相等可得OE=OF,再根据对角线互相平分的四边形是平行四边形证明即可;(2)设OM=x,根据∠MBO的正切值表示出BM,再根据△AOM和△OBM相似,利用相似三角形对应边成比例求出AM,然后根据△AEM和△BFM相似,利用相似三角形对应边成比例求解即可.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
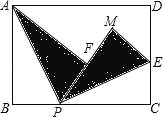
【题目】如图,矩形纸片ABCD的边AB=3,BC=4,点P是BC边上一动点(不与B、C重合),现将△ABP沿AP翻折,得到△AFP,再在CD边上选择适当的点E,将△PCE沿PE翻折,得到△PME,且直线PF、PM重合,若点F落在矩形纸片的内部,则CE的最大值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校需要购买一批篮球和足球,已知一个篮球比一个足球的价格高30元.买两个篮球和三个足球共需510元.
(1)求篮球和足球的单价;
(2)根据需要,学校决定购买篮球和足球共100个,其中篮球的数量不少于足球数量的![]() ,用于购买这批篮球和足球的资金不超过10300元,请问有哪几种购买方案?并指出其中费用最低的方案.
,用于购买这批篮球和足球的资金不超过10300元,请问有哪几种购买方案?并指出其中费用最低的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】环境监测中PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.如果1微米=0.000001米,那么数据0.0000025用科学记数法可以表示为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com