
如图,正方形ABCD的边长为4,E是BC边的中点,点P在射线AD上,过P作PF⊥AE于F.
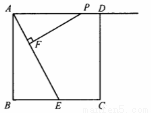
(1)求证:△PFA∽△ABE;
(2)若AP=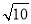 ,求△PFA的面积
,求△PFA的面积
(1)证明见解析;(2)2.
【解析】
试题分析:(1)由正方形的性质就可以得出∠B=∠C=∠ADC=∠BAD=90°AD∥BC,就可以得出∠PAF=∠AEB,就可以得出△PFA∽△ABE;
(2)根据勾股定理可以求出AE的值及△ABE的面积,由相似三角形的性质就可以求出结论.
试题解析:(1)∵四边形ABCD是正方形,
∴∠B=∠C=∠ADC=∠BAD=90°AD∥BC,AB=BC=CD=DA=4,
∴∠DAE=∠AEB.
∵PF⊥AE,
∴∠AFP=90°,
∴∠AFP=∠B
∴△PFA∽△ABE
(2)∵E是BC边的中点,
∴BE=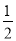 BC=2.
BC=2.
在Rt△ABE中,由勾股定理,得
AE=2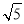 .
.
∵△PFA∽△ABE,
∴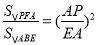 .
.
∵S△ABE=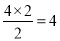 ,
,
∴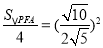
∴S△PFA=2.
答:△PFA的面积为2.
考点:1.相似三角形的判定与性质;2.正方形的性质.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案科目:初中数学 来源:2014-2015学年辽宁省丹东市九年级上学期第二次月考数学试卷(解析版) 题型:填空题
如图,正方形ABCD和正方形CEFG中,D在CG上,BC=1,CG=3,H是AF的中点,则CH的长是 。

查看答案和解析>>
科目:初中数学 来源:2014-2015学年河北省沙河市九年级上学期期末模拟考试数学试卷(解析版) 题型:解答题
为了落实国家的惠农政策,某地政府制定了农户投资购买收割机的补贴办法,其中购买Ⅰ、Ⅱ两型收割机所投资的金额与政府补贴的额度存在下表所示的函数对应关系:
Ⅰ型收割机 | Ⅱ型收割机 | ||||
投资金额x(万元) | x | 5 | x | 2 | 4 |
补贴金额y(万元) | y1=kx | 2 | y2=ax2+bx | 2.4 | 3.2 |
(1)分别求出y1和y2的函数表达式;
(2)旺叔准备投资10万元购买Ⅰ、Ⅱ两型收割机。请你设计一个能获得最大补贴金额的方案,并求出按此方案能获得的补贴金额。
查看答案和解析>>
科目:初中数学 来源:2014-2015学年河北省沙河市九年级上学期期末模拟考试数学试卷(解析版) 题型:选择题
两圆的圆心坐标分别为(3,0)、(0,4),直径分别为4和6,则这两圆的位置关系是( )
A.外离 B.相交 C.外切 D.内切
查看答案和解析>>
科目:初中数学 来源:2014-2015学年河北省沙河市九年级上学期第二次月度联考数学试卷(解析版) 题型:选择题
若三角形的三边分别为a,b,c,则下面四种情况中,构成直角三角形的是( )
A.a=2,b=3,c=4 B.a=12,b=5,c=13
C.a=4,b=5,c=6 D.a=7,b=18,c=17
查看答案和解析>>
科目:初中数学 来源:2014-2015学年河北省沙河市九年级上学期第四次月考数学试卷(解析版) 题型:选择题
二次函数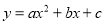 的图象如图所示,则下面四个结论中正确的结论有( )
的图象如图所示,则下面四个结论中正确的结论有( )
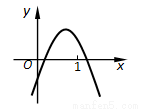
①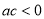 ;②
;②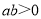 ;③
;③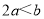 ;④
;④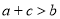 ;⑤
;⑤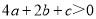 ;⑥
;⑥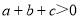 .
.
A.2个 B.3个 C.4个 D.5个
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省龙岩市九年级上学期半期考试数学试卷(解析版) 题型:选择题
下列方程,是一元二次方程的是( )
①3x2+x=20,②2x2-3xy+4=0,③x2- =4,④x2=0,⑤x2-
=4,④x2=0,⑤x2- +3=0
+3=0
A.①② B.①②④⑤ C.①③④ D.①④⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com