
【题目】某中学开展“绿化家乡、植树造林”活动,为了解全校植树情况,对该校甲、乙、丙、丁四个班级植树情况进行了调查,将收集的数据整理并绘制成图1和图2两幅尚不完整的统计图,请根据图中的信息,完成下列问题:
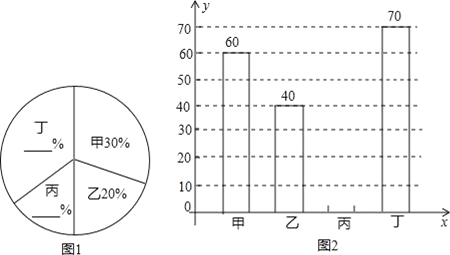
(1)这四个班共植树 棵;
(2)补全两幅统计图;
(3)求图1中“甲”班级所对应的扇形圆心角的度数;
(4)若四个班级所种植的树成活了190棵,全校共植树2000棵,请你估计全校种植的树中成活的树有多少棵.
【答案】(1)200;(2)补图见解析;(3)图1中“甲”班级所对应的扇形圆心角的度数为 108°;(4)全校种植的树中成活的树有1900棵.
【解析】试题分析:(1)根据乙班的植树初除以乙班所占的百分比,可得答案;
(2)根据有理数的减法,可得丙班的指数,根据丙班的指数除以总植树的棵数,丁班的指数除以总植树的棵数,可得答案;
(3)用360°乘以图1中“甲”班级的百分比即可得;
(4)根据样本估计总体,可得答案.
试题解析:(1)这四个班共植树40÷20%=200(棵),
(2)丙班植树200﹣60﹣40﹣70=30棵,丙班所占的百分比![]() =15%,丁班所占的百分比70÷200=35%,
=15%,丁班所占的百分比70÷200=35%,
如图所示:
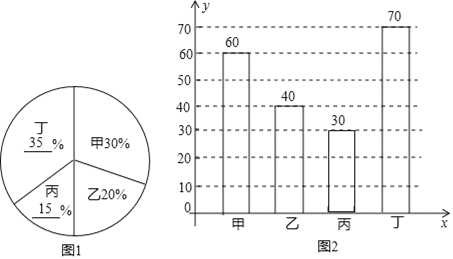 ,
,
(3)图1中“甲”班级所对应的扇形圆心角的度数为:360°×30%=108°;
(4)2000×![]() =1900棵,
=1900棵,
答:全校种植的树中成活的树有1900棵.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】小王在下面的计算中只做对了一道题,他做对的题目是( )
A.3a72a6=6a42
B.(a7)6=a42
C.a42÷a7=a6
D.a6+a6=a12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,AC交BD于点O,且AB∥CD,给出以下四种说法:
①如果再加上条件“BC=AD”,那么四边形ABCD一定是平行四边形;
②如果再加上条件“∠BAD=∠BCD”,那么四边形ABCD一定是平行四边形;
③如果再加上条件“AO=OC”,那么四边形ABCD一定是平行四边形;
④如果再加上条件“∠DBA=∠CAB”,那么四边形ABCD一定是平行四边形.
其中正确的说法是( )
A.①②
B.①③④
C.②③
D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,对角线AC,BD相交于点O,给出下列四组条件:
①AB∥CD,AD∥BC;
②AB=CD,AD=BC;
③AO=CO,BO=DO;
④AB∥CD,AD=BC.
其中一定能判定这个四边形是平行四边形的条件有( )
A.1组
B.2组
C.3组
D.4组
查看答案和解析>>
科目:初中数学 来源: 题型:
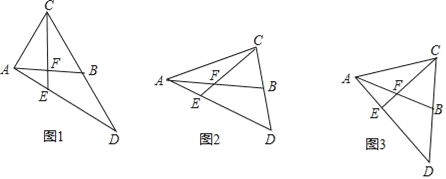
【题目】已知,在等腰△ABC中,AB=AC,F为AB边上的中点,延长CB至D,使得BD=BC,连接AD交CF的延长线于E.
(1)如图1,若∠BAC=60°,求证:△CED为等腰三角形
(2)如图2,若∠BAC≠60°,(1)中结论还成立吗?若成立,请证明,若不成立,请说明理由.
(3)如图3,当![]() = 是(直接填空),△CED为等腰直角三角形.
= 是(直接填空),△CED为等腰直角三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com