
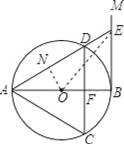
如图,AB是⊙O的直径,过点B作⊙O的切线BM,弦CD∥BM,交AB于点F,且DA=DC,链接AC,AD,延长AD交BM地点E.
(1)求证:△ACD是等边三角形.
(2)连接OE,若DE=2,求OE的长.
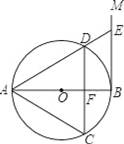

【考点】切线的性质.
【分析】(1)由AB是⊙O的直径,BM是⊙O的切线,得到AB⊥BE,由于CD∥BE,得到CD⊥AB,根据垂径定理得到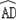
 =
=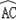
 ,于是得到AD=AC,然后根据已知DA=DC,得出AD=AC=CD,即可证得;
,于是得到AD=AC,然后根据已知DA=DC,得出AD=AC=CD,即可证得;
(2)连接OE,过O作ON⊥AD于N,由(1)知,△ACD是等边三角形,得到∠DAC=60°又直角三角形的性质得到BE=
 AE,ON=
AE,ON=
 AO,设⊙O的半径为:r则ON=
AO,设⊙O的半径为:r则ON=
 r,AN=DN=
r,AN=DN=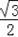
 r,由于得到EN=2+
r,由于得到EN=2+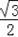
 r,BE=AE=
r,BE=AE=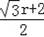
 ,在Rt△DEF与Rt△BEO中,由勾股定理列方程即可得到结论.
,在Rt△DEF与Rt△BEO中,由勾股定理列方程即可得到结论.
【解答】(1)证明:∵AB是⊙O的直径,BM是⊙O的切线,
∴AB⊥BE,
∵CD∥BE,
∴AB⊥CD,
∴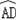
 =
=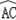
 ,
,
∴AD=AC,
∵DA=DC,
∴AD=AC=CD,
∴△ACD是等边三角形;
(2)解:连接OE,过O作ON⊥AD于N,由(1)知,△ACD是等边三角形,
∴∠DAC=60°
∵AD=AC,CD⊥AB,
∴∠DAB=30°,
∴BE=
 AE,ON=
AE,ON=
 AO,
AO,
设⊙O的半径为:r,
∴ON=
 r,AN=DN=
r,AN=DN=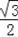
 r,
r,
∴EN=2+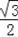
 r,BE=
r,BE=
 AE=
AE=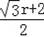
 ,
,
在Rt△NEO与Rt△BEO中,
OE2=ON2+NE2=OB2+BE2,
即(
 )2+(2+
)2+(2+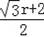
 )2=r2+(
)2=r2+(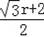
 )2,
)2,
∴r=2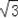
 ,
,
∴OE2=(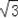
 )2+25=28,
)2+25=28,
∴OE=2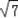
 .
.

【点评】本题考查了切线的性质,垂径定理,等边三角形的判定,直角三角形的性质,勾股定理,过O作ON⊥AD于N,构造直角三角形是解题的关键.


 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:
某公司购进一种化工原料若干千克,价格为每千克30元,物价部门规定其销售单价每千克不高于60元且不低于30元,经市场调查发现,日销售量y(千克)是销售单价x(元)的一次函数,且当x=60时,y=80,当x=50时,y=100.
(1)求y与x的函数解析式;
(2)求该公司销售该原料日获利w(元)与销售单价x(元)之间的函数解析式;
(3)求当销售单价为多少元时,该公司日获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
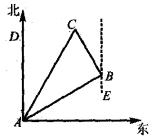
3、如图所示,在一次夏令营活动中,小明从营地A点出发,沿北偏东60°方向走了 到达B点,然后再沿北偏西30°方向走了500m到达目的地C点。
到达B点,然后再沿北偏西30°方向走了500m到达目的地C点。
(1)求A、C两点之间的距离。
(2)确定目的地C在营地A的什么方向。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com