
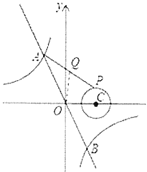
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于A,B两点,点P在以
的图象交于A,B两点,点P在以![]() 为圆心,1为半径的⊙C上,Q是AP的中点,已知OQ长的最小值为
为圆心,1为半径的⊙C上,Q是AP的中点,已知OQ长的最小值为![]() ,则
,则![]() 的值为______.
的值为______.
【答案】![]()
【解析】
作辅助线,先确定OQ长的最小时,点P的位置,当BP延长线过圆心C时,BP最短,设B(t,-2t),则CD=2-t,BD=2t,根据勾股定理计算t的值,可得k的值.
解:连接BP,
由对称性得:OA=OB,
∵Q是AP的中点,
∴OQ=![]() BP,
BP,
∵OQ长的最小值为![]() ,
,
∴BP长的最小值为![]() ×2=1,
×2=1,
如图,当BP的延长线过圆心C时,BP最短,过B作BD⊥x轴于D,
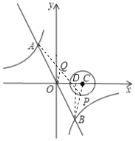
∵CP=1,
∴BC=2,
∵B在直线y=-2x上,
设B(t,-2t),则CD=2-t,BD=2t,
在Rt△BCD中,由勾股定理得:BC2=CD2+BD2,
∴22=(2-t)2+(2t)2,
∴t=0(舍)或![]() ,
,
∴B(![]() ,-
,-![]() ),
),
∵点B在反比例函数y=![]() (k<0)的图象上,
(k<0)的图象上,
![]()
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】某公园要建造一个圆形的喷水池,在水池中央垂直于水面竖一根柱子,上面的A处安装一个喷头向外喷水.连喷头在内,柱高0.8m.水流在各个方向上沿形状相同的抛物线路径落下,如图(1)所示.
根据设计图纸已知:如图(2)中所示直角坐标系中,水流喷出的高度y(m)与水平距离x(m)之间的函数关系式是 y=﹣x2+2x+![]() .
.
(1)喷出的水流距水平面的最大高度是多少?
(2)如果不计其他因素,那么水池半径至少为多少时,才能使喷出的水流都落在水池内?
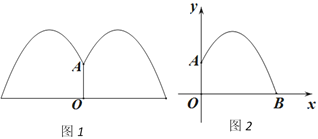
查看答案和解析>>
科目:初中数学 来源: 题型:
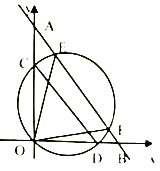
【题目】如图,在平面直角坐标系中,直线![]() 交y轴于点A,交x轴于点B,点C在线段OA上,点D在线段OB上,且
交y轴于点A,交x轴于点B,点C在线段OA上,点D在线段OB上,且![]() ,点C、D不与点O重合,以CD为直径的圆交直线AB于两点E、F,连接OE、OF,则当
,点C、D不与点O重合,以CD为直径的圆交直线AB于两点E、F,连接OE、OF,则当![]() 的面积的最大时,线段EF的长是________.
的面积的最大时,线段EF的长是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
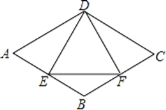
【题目】如图,在菱形ABCD中,E是AB边上一点,且∠A=∠EDF=60°,有下列结论:①AE=BF;②△DEF是等边三角形;③△BEF是等腰三角形;④∠ADE=∠BEF,其中结论正确的个数是( )
A.3
B.4
C.1
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【阅读理解】
某科技公司生产一种电子产品,该产品总成本包括技术成本、制造成本、销售成本三部分。经核算,2016年该产品各部分成本所占比例约为2:a:1,且2016年该产品的技术成本、制造成本分别为400万元、1400万元。
(1)确定a的值,并求2016年产品总成本为多少万元。
(2)为降低总成本,该公司2017年及2018年增加了技术投入,确保这两年技术成本都比前一年增加一个相同的百分数m(m<50%),制造成本在这两年里都比前一年减少一个相同的百分数2m;同时为了扩大销售量,2018年的销售成本将在2016年的基础上提高10%,经过以上变革,预计2018年该产品总成本达到2016年该产品总成本的![]() 。求m的值。
。求m的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级学生小丽,小强和小红到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作,已知该水果的进价为8元/千克,下面是他们在活动结束后的对话.
小丽:如果以10元/千克的价格销售,那么每天可售出300千克.
小强:如果以13元/千克的价格销售,那么每天可获取利润750元.
小红:我通过调查验证发现每天的销售量![]() (千克)与销售单价
(千克)与销售单价![]() (元)之间存在一次函数关系.
(元)之间存在一次函数关系.
(1)求![]() (千克)与
(千克)与![]() (元)
(元)![]() 的函数关系式.
的函数关系式.
(2)当销售单价为何值时,该超市销售这种水果每天获得的利润达600元?[利润=销售量×(销售单价﹣进价)].
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]()
![]() 的顶点为(m
的顶点为(m![]() ,n
,n![]() )抛物线
)抛物线![]() 的顶点为(m
的顶点为(m![]() ,n
,n![]() ),如果
),如果![]() ,那么我们称抛物线
,那么我们称抛物线![]() 与
与![]() 关于点
关于点![]() 中心对称,给出抛物线①
中心对称,给出抛物线①![]() ;②
;②![]()
(1)判断抛物线①与抛物线②是否中心对称?若是,求出对称中心的坐标;若不是,说明理由;
(2)直线y=m交抛物线①于A. B两点,交抛物线②于C. D两点,如果AB=2CD,求m的值;
(3)设抛物线①与抛物线②的顶点分别为M、N,点P在x轴上移动,若△MNP为直角三角形,求点P坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位为了创建城市文明单位,准备在单位的墙(线段MN所示)外开辟一处长方形的上地进行绿化美化,除墙体外三面要用栅栏围起来,计划用栅栏50米,设AB的长为x米,长方形的面积为y平方米.
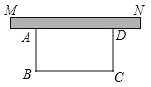
(1)请求出y与x的函数关系式(不需写出自变量的取值范围)
(2)不考虑墙体长度,问AB的长为多少时,长方形的面积最大?
(3)若墙体长度为20米,问长方形面积最大是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
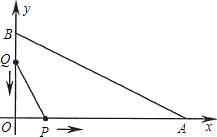
【题目】在平面直角坐标系中,已知OA=10cm,OB=5cm,点P从点O开始沿OA边向点A以2cm/s的速度移动;点Q从点B开始沿BO边向点O以1cm/s的速度移动.如果P、Q同时出发,用t(s)表示移动的时间(0≤t≤5),
(1)用含t的代数式表示:线段PO= cm;OQ= cm.
(2)当t为何值时,四边形PABQ的面积为19cm2.
(3)当△POQ与△AOB相似时,求出t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com