
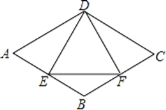
【题目】如图,在菱形ABCD中,E是AB边上一点,且∠A=∠EDF=60°,有下列结论:①AE=BF;②△DEF是等边三角形;③△BEF是等腰三角形;④∠ADE=∠BEF,其中结论正确的个数是( )
A.3
B.4
C.1
D.2
【答案】A
【解析】
首先连接BD,易证得△ADE≌△BDF,然后可证得DE=DF,AE=BF,即可得△DEF是等边三角形,然后可证得∠ADE=∠BEF.
连接BD,
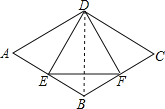
∵四边形ABCD是菱形,
∴AD=AB,∠ADB=![]() ∠ADC,AB∥CD,
∠ADC,AB∥CD,
∵∠A=60°,
∴∠ADC=120°,∠ADB=60°,
同理:∠DBF=60°,
即∠A=∠DBF,
∴△ABD是等边三角形,
∴AD=BD,
∵∠ADE+∠BDE=60°,∠BDE+∠BDF=∠EDF=60°,
∴∠ADE=∠BDF,
∵在△ADE和△BDF中,
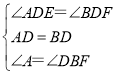 ,
,
∴△ADE≌△BDF(ASA),
∴DE=DF,AE=BF,故①正确;
∵∠EDF=60°,
∴△EDF是等边三角形,
∴②正确;
∴∠DEF=60°,
∴∠AED+∠BEF=120°,
∵∠AED+∠ADE=180°-∠A=120°,
∴∠ADE=∠BEF;
故④正确;
∵△ADE≌△BDF,
∴AE=BF,
同理:BE=CF,
但BE不一定等于BF,
故③错误.
综上所述,结论正确的是①②④.
故选A.


科目:初中数学 来源: 题型:
【题目】如图,在7×7网格中,每个小正方形边长都为1.建立适当的平面直角坐标系,使点A(3,4)、C(4,2).

(1)判断△ABC的形状,并求图中格点△ABC的面积;
(2)在x轴上有一点P,使得PA+PC最小,则PA+PC的最小值为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AD//BC,∠B=70°,∠C=40°,DE//AB交BC于点E.若AD=3cm,BC=10cm,则CD的长是 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某区九年级学生课外体育活动的情况,从该年级学生中随机抽取了4%的学生,对其参加的体育活动项目进行了调查,将调查的数据进行统计并绘制成如图所示的扇形统计图和条形统计图.有下列结论:①被抽测学生中参加羽毛球项目的人数为30;②在本次调查中“其他”的扇形的圆心角的度数为36°;③估计全区九年级参加篮球项目的学生比参加足球项目的学生多20%;④全区九年级大约有1500名学生参加乒乓球项目.其中正确结论的个数是( )

A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠B=60°,D、E分别为AB、BC上的点,且AE、CD交于点F.
(1)如图1,若AE、CD为△ABC的角平分线:
①求∠AFD的度数;
②若AD=3,CE=2,求AC的长;
(2)如图2,若∠EAC=∠DCA=30°,求证:AD=CE.

查看答案和解析>>
科目:初中数学 来源: 题型:
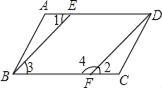
【题目】如图,已知AD∥BC,∠3+∠4=180°,要证∠1=∠2,请完善证明过程,并在括号内填上相应依据:
∵AD∥BC(已知)
∴∠l=∠3( ),
∵∠3+∠4=180°(已知),
∴BE∥DF( ),
∴ = ( ).
∴∠1=∠2( ).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com