
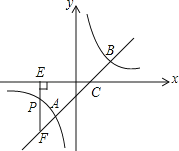
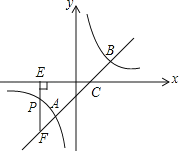
【题目】如图,直线y=x﹣1与反比例函数y=![]() 的图象交于A、B两点,与x轴交于点C,已知点A的坐标为(﹣1,m).
的图象交于A、B两点,与x轴交于点C,已知点A的坐标为(﹣1,m).
(1)求反比例函数的解析式;
(2)若点P(n,﹣1)是反比例函数图象上一点,过点P作PE⊥x轴于点E,延长EP交直线AB于点F,求△CEF的面积.
(3)在x轴上是否存在点Q,使得△QBC是等腰三角形?若存在,请直接写出Q点坐标;若不存在,请说明理由.
【答案】(1)反比例函数的表达式为:y=![]() .(2)
.(2)![]() (3)在x轴上存在点Q,使得△QBC是等腰三角形,Q点坐标为(1+
(3)在x轴上存在点Q,使得△QBC是等腰三角形,Q点坐标为(1+![]() ,0)、(1﹣
,0)、(1﹣![]() ,0)、(2,0)或(3,0).
,0)、(2,0)或(3,0).
【解析】
试题分析:(1)将点A的坐标代入直线AB的解析式中即可求出m的值,根据点A的坐标利用反比例函数图象上点的坐标特征即可求出k值,从而得出反比例函数解析式;
(2)由直线AB的解析式可求出点C的坐标,将点P的坐标代入反比例函数解析式中可求出n值,从而可得出点E、F的坐标,由此可得出线段EF、CE的长度,再根据三角形的面积公式即可得出结论;
(3)假设存在,设点Q的坐标为(a,0).联立直线AB与反比例函数解析式可求出点B的坐标,由此即可得出线段BC、BQ、CQ的长,根据等腰三角形的性质分BC=BQ、BC=CQ以及BQ=CQ三种情况考虑,由此可得出关于a的方程,解方程即可求出点Q的坐标,此题得解.
解:(1)把A(﹣1,m)代入y=x﹣1,
∴m=﹣2,
∴A(﹣1,﹣2).
∵点A在反比例函数图象上,
∴k=﹣1×(﹣2)=2,
∴反比例函数的表达式为:y=![]() .
.
(2)令y=x﹣1中y=0,则0=x﹣1,解得:x=1,
∴C(1,0).
把P(n,﹣1)代入y=![]() 中,得:﹣1=
中,得:﹣1=![]() ,
,
解得:n=﹣2,
∴P(﹣2,﹣1).
∵PE⊥x轴,
∴E(﹣2,0).
令y=x﹣1中x=﹣2,则y=﹣2﹣1=﹣3,
∴F(﹣2,﹣3).
∴CE=3,EF=3,
∴S△CEF=![]() CEEF=
CEEF=![]() .
.
(3)假设存在,设点Q的坐标为(a,0).
联立直线AB和反比例函数解析式得: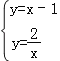 ,
,
解得:![]() 或
或![]() ,
,
∴B(2,1).
∴BC=![]() =
=![]() ,CQ=|a﹣1|,BQ=
,CQ=|a﹣1|,BQ=![]() .
.
△QBC是等腰三角形分三种情况:
①当BC=CQ时,有![]() =|a﹣1|,
=|a﹣1|,
解得:a1=1+![]() ,a2=1﹣
,a2=1﹣![]() ,
,
此时点Q的坐标为(1+![]() ,0)或(1﹣
,0)或(1﹣![]() ,0);
,0);
②当CQ=BQ时,有|a﹣1|=![]() ,
,
解得:a3=2,
此时点Q的坐标为(2,0);
③当BC=BQ时,有![]() =
=![]() ,
,
解得:a4=3,a5=1,
此时点Q的坐标为(3,0)或(1,0)(舍去).
综上可知:在x轴上存在点Q,使得△QBC是等腰三角形,Q点坐标为(1+![]() ,0)、(1﹣
,0)、(1﹣![]() ,0)、(2,0)或(3,0).
,0)、(2,0)或(3,0).


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:
【题目】计算:
①(﹣2x)(4x2﹣2x+1) ②(6a3﹣4a2+2a)÷2a
③a4 +(a2)4 -(a2)2 ④![]()
⑤(2a+b)2 ⑥ (3x+7y)(3x-7y)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下是某校九年级10名同学参加学校演讲比赛的统计表:
成绩/分 | 80 | 85 | 90 | 95 |
人数/人 | 1 | 2 | 5 | 2 |
则这组数据的中位数和平均数分别为( )
A. 90,90 B. 90,89 C. 85,89 D. 85,90
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学在本学期的前四次数学测验中得分依次是95,82,76,88,马上要进行第五次测验了,他希望五次成绩的平均分能达到85分,那么这次测验他应得( )分.
A.84 B.75 C.82 D.87
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD.已知DE=6,∠BAC+∠EAD=180°,则弦BC的弦心距等于 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知两个完全相同的直角三角形纸片△ABC、△DEF,如图1放置,点B、D重合,点F在BC上,AB与EF交于点G.∠C=∠EFB=90°,∠E=∠ABC=30°,现将图1中的△ABC绕点F按每秒10°的速度沿逆时针方向旋转180°,在旋转的过程中,△ABC恰有一边与DE平行的时间为___________s

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com