
【题目】【问题探究】
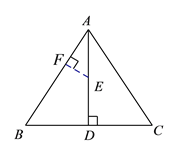
(![]() )如图①,点
)如图①,点![]() 是正
是正![]() 高
高![]() 上的一定点,请在
上的一定点,请在![]() 上找一点
上找一点![]() ,使
,使![]() ,并说明理由.
,并说明理由.
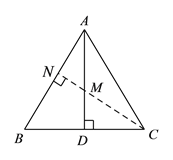
(![]() )如图②,点
)如图②,点![]() 是边长为
是边长为![]() 的正
的正![]() 高
高![]() 上的一动点,求
上的一动点,求![]() 的最小值.
的最小值.
【问题解决】
(![]() )如图③,
)如图③,![]() 、
、![]() 两地相距
两地相距![]() ,
, ![]() 是笔直第沿东西方向向两边延伸的一条铁路.今计划在铁路线
是笔直第沿东西方向向两边延伸的一条铁路.今计划在铁路线![]() 上修一个中转站
上修一个中转站![]() ,再在
,再在![]() 间修一条笔直的公路.如果同样的物资在每千米公路上的运费是铁路上的两倍.那么,为使通过铁路由
间修一条笔直的公路.如果同样的物资在每千米公路上的运费是铁路上的两倍.那么,为使通过铁路由![]() 到
到![]() 再通过公路由
再通过公路由![]() 到
到![]() 的总运费达到最小值,请确定中转站
的总运费达到最小值,请确定中转站![]() \的位置,并求出
\的位置,并求出![]() 的长.(结果保留根号)
的长.(结果保留根号)

【答案】(![]() )见解析;(
)见解析;(![]() )
)![]() ;(
;(![]() )
)![]() .
.
【解析】(1)根据等边三角形的性质得出∠BAD=30°,得出EF=![]() AE;
AE;
(2)根据题意得出C,M,N在一条直线上时,此时![]() AM+MC最小,进而求出即可;
AM+MC最小,进而求出即可;
(3)作BD⊥AC,垂足为点D,在AC异于点B的一侧作∠CAN=30°,作BF⊥AN,垂足为点F,交AC于点M,点M即为所求,在Rt△ABD中,求出AD的长,在Rt△MBD中,得出MD的长,即可得出答案.
解:(![]() )过点
)过点![]() 作
作![]() 于
于![]() ,点
,点![]() 即为所求.
即为所求.
证明:∵![]() 为正
为正![]() ,
, ![]() ,
,
∴![]() .
.
(![]() )在
)在![]() 中,
中, ![]() ,
,
如图,作![]() 于
于![]() ,交
,交![]() 于
于![]() ,
,
由(![]() )可知
)可知![]() ,
,
∴![]() 最小
最小![]() .
.
(![]() )如图,作
)如图,作![]() 于
于![]() .
.
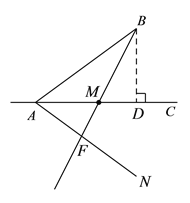
在![]() 点另一侧作
点另一侧作![]() ,
,
作![]() 于
于![]() ,交
,交![]() 于
于![]() ,点
,点![]() 即为所求.
即为所求.
在![]() 中,
中, ![]() ,
, ![]() .
.
∴![]() .
.
在![]() 中,
中, ![]() ,
,
∴![]() ,
,
∴![]() ,
,
![]() .
.
“点睛”此题主要考查了正三角形的性质以及锐角三角函数关系和勾股定理等知识,利用特殊角的三角函数关系得出是解题关键.


科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线相交于点O,AC=2,BD=2![]() ,将菱形按如图方式折叠,使点B与点O重合,折痕为EF,则五边形AEFCD的周长为_____________
,将菱形按如图方式折叠,使点B与点O重合,折痕为EF,则五边形AEFCD的周长为_____________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班级为准备元旦联欢会,欲购买价格分别为2元、4元和10元的三种奖品,每种奖品至少购买一件,共买16件,恰好用50元.若2元的奖品购买a件.
(1)用含a的代数式表示另外两种奖品的件数;
(2)请你设计购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请从以下两个小题中任选一个作答,若多选,按选做的第一题计分.
A:如图1,AD是正五边形ABCDE的一条对角线,则∠BAD= .
B:如图2,小明从坡角为27.5°的斜坡的坡底A走到离A水平距离10米远(AC=10米)的C处,则他走过的坡面距离AB为 米(结果精确到0.01米)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1已知:∠B=25°,∠BED=80°,∠D=55°.探究AB与CD有怎样的位置关系.
(2)如图2已知AB∥EF,试猜想∠B,∠F,∠BCF之间的关系,写出这种关系,并加以证明.
(3)如图3已知AB∥CD,试猜想∠1,∠2,∠3,∠4,∠5之间的关系,请直接写出这种关系,不用证明.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知直线y=2x分别与双曲线![]() ,
, ![]() 交于P、Q(1,n)两点.
交于P、Q(1,n)两点.
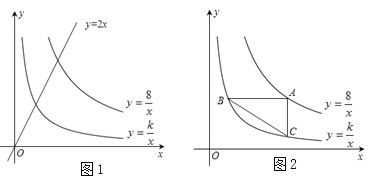

(1)求k的值.
(2)如图2,点A是双曲线![]() 上的动点,AB∥x轴,AC∥y轴,分别交双曲线
上的动点,AB∥x轴,AC∥y轴,分别交双曲线![]() 于点B、C,连接BC.试探索在点A运动过程中,△ABC的面积是否变化?若不变,请求出△ABC的面积;若改变,请说明理由;
于点B、C,连接BC.试探索在点A运动过程中,△ABC的面积是否变化?若不变,请求出△ABC的面积;若改变,请说明理由;
(3)如图3,过点B作AC的平行线交直线y=2x于点D,请你进一步探索在点A运动过程中,tan∠ACB=tan∠ADB能否成立?若能,求出此时点A的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节三天假期的某一天,小明全家上午8时自驾小汽车从家里出发,到章丘某旅游景点游玩.该小汽车离家的距离S(千米)与时间t(小时)的关系如图所示.根据图象提供的有关信息,下列说法中错误的是( )

A. 景点离小明家180千米 B. 小明到家的时间为17点
C. 返程的速度为60千米每小时 D. 10点至14点,汽车匀速行驶
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△AOB中,AB⊥OB,且AB=OB=3,设直线![]() 截此三角形所得阴影部分的面积为S,则S与t之间的函数关系的图象为下列选项中的( )
截此三角形所得阴影部分的面积为S,则S与t之间的函数关系的图象为下列选项中的( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
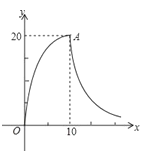
【题目】最近流感高发期,在预防流感期间学校坚持天天消毒,下图是某次消毒时教室内空气中消毒液浓度 y(单位:毫克/立方米)随时间 x(单位:分钟)的变化情况图.从开始喷药到喷药结束的 10 分钟内(包括第十分钟),y 是 x 的二次函数;喷药结束后(从第十分钟开始),y 是 x 的反比例函数.
(1)如果点 A 是图中二次函数的顶点,求二次函数和反比例函数的解析式 (要写出自变量取值范围);
(2)已知空气中消毒液浓度 y 不少于 15 毫克/立方米且持续时间不少于 8 分钟才能有效消毒,通过计算,请你回答这次消毒是否有效?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com