
【题目】如图1,已知直线y=2x分别与双曲线![]() ,
, ![]() 交于P、Q(1,n)两点.
交于P、Q(1,n)两点.
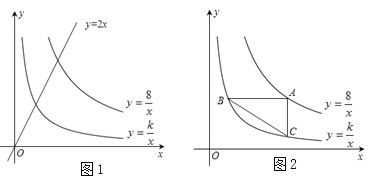

(1)求k的值.
(2)如图2,点A是双曲线![]() 上的动点,AB∥x轴,AC∥y轴,分别交双曲线
上的动点,AB∥x轴,AC∥y轴,分别交双曲线![]() 于点B、C,连接BC.试探索在点A运动过程中,△ABC的面积是否变化?若不变,请求出△ABC的面积;若改变,请说明理由;
于点B、C,连接BC.试探索在点A运动过程中,△ABC的面积是否变化?若不变,请求出△ABC的面积;若改变,请说明理由;
(3)如图3,过点B作AC的平行线交直线y=2x于点D,请你进一步探索在点A运动过程中,tan∠ACB=tan∠ADB能否成立?若能,求出此时点A的坐标;若不能,请说明理由.
【答案】(1)k的值为2; (2)不变;(3)能成立.当tan∠ADB= tan∠ACB时,A点的坐标为(2![]() ,
, ![]() )或(2,4).
)或(2,4).
【解析】试题分析:(1)将点Q(1,n)代入y=2x得求得n的值,再将点Q坐标代入![]() ,可得k的值;
,可得k的值;
(2)设点A的坐标为(a,b),易得b=![]() ,结合条件可用a的代数式表示点B、点C的坐标,进而表示出线段AB、AC的长,就可算出△BAC的面积是一个定值;
,结合条件可用a的代数式表示点B、点C的坐标,进而表示出线段AB、AC的长,就可算出△BAC的面积是一个定值;
(3)由an∠ADB= tan∠ACB可得![]() ,DB=AC,设出点A的坐标,则可得到相应B、D的坐标,进而表示出AC、BD,即可求得a的值.
,DB=AC,设出点A的坐标,则可得到相应B、D的坐标,进而表示出AC、BD,即可求得a的值.
试题解析:(1)将点Q(1,n)代入y=2x得:n=2×1=2,
将点Q(1,2)代入![]() 得:k=2×1=2,
得:k=2×1=2,
∴k的值为2;
(2)不变.
由题意设点A的坐标为(a, ![]() ),
),
∵AB∥x轴,AC∥y轴,
∴xC=xA=a,yB=yA=b=![]() .
.
∵点B、C在双曲线y=![]() 上,
上,
∴xB=![]() =,yC=
=,yC=![]() .
.
∴点B的坐标为(![]() ,
, ![]() ),点C的坐标为(a,
),点C的坐标为(a, ![]() ).
).
∴AB= ![]() ,AC=
,AC=![]() .
.
∴S△ABC=![]() ABAC=
ABAC=![]() .
.
∴在点A运动过程中,△ABC的面积不变,始终等于![]() .
.
(3)能成立.
∵tan∠ADB= tan∠ACB, ![]() ,DB=AC,
,DB=AC,
由题意设点A的坐标为(a, ![]() ),则:
),则:
B(![]() ,
, ![]() )、C(a,
)、C(a, ![]() )、D(
)、D(![]() ,
, ![]() )
)
∴AC=![]() ,DB=
,DB=![]()
![]()
∴![]()
![]() =
=![]()
解得: ![]() ,
, ![]() (舍),
(舍),![]() ,
, ![]() (舍)
(舍)
∴点A的坐标为(2![]() ,
, ![]() )或(2,4).
)或(2,4).
综上所述:当tan∠ADB= tan∠ACB时,A点的坐标为(2![]() ,
, ![]() )或(2,4
)或(2,4
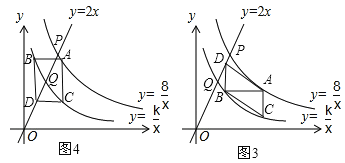
备注:当点A为(2![]() ,
, ![]() )时,如图3所示;
)时,如图3所示;
当点A为(2,4)时,如图4所示.


科目:初中数学 来源: 题型:
【题目】如图所示,抛物线y=ax2+bx+c与直线y=﹣x+6分别交于x轴和y轴上同一点,交点分别是点B和点C,且抛物线的对称轴为直线x=4.
(1)求出抛物线与x轴的两个交点A,B的坐标.
(2)试确定抛物线的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F.
(1)求证:△ABE≌△CDF;
(2)若AB=DB,猜想:四边形DFBE是什么特殊的四边形?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
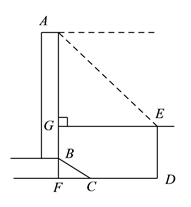
【题目】如图所示,某办公大楼正前方有一根高度是![]() 米的旗杆
米的旗杆![]() ,从办公楼顶端
,从办公楼顶端![]() 测得旗杆顶端
测得旗杆顶端![]() 的俯角
的俯角![]() 是
是![]() ,旗杆底端
,旗杆底端![]() 到大楼前梯坎底边的距离
到大楼前梯坎底边的距离![]() 是
是![]() 米,梯坎坡长
米,梯坎坡长![]() 是
是![]() 米,梯坎坡度
米,梯坎坡度![]() ,求大楼
,求大楼![]() 的高度.(精确到
的高度.(精确到![]() 米,参与数据:
米,参与数据: ![]() ,
, ![]() ,
, ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题探究】
(![]() )如图①,点
)如图①,点![]() 是正
是正![]() 高
高![]() 上的一定点,请在
上的一定点,请在![]() 上找一点
上找一点![]() ,使
,使![]() ,并说明理由.
,并说明理由.
(![]() )如图②,点
)如图②,点![]() 是边长为
是边长为![]() 的正
的正![]() 高
高![]() 上的一动点,求
上的一动点,求![]() 的最小值.
的最小值.
【问题解决】
(![]() )如图③,
)如图③,![]() 、
、![]() 两地相距
两地相距![]() ,
, ![]() 是笔直第沿东西方向向两边延伸的一条铁路.今计划在铁路线
是笔直第沿东西方向向两边延伸的一条铁路.今计划在铁路线![]() 上修一个中转站
上修一个中转站![]() ,再在
,再在![]() 间修一条笔直的公路.如果同样的物资在每千米公路上的运费是铁路上的两倍.那么,为使通过铁路由
间修一条笔直的公路.如果同样的物资在每千米公路上的运费是铁路上的两倍.那么,为使通过铁路由![]() 到
到![]() 再通过公路由
再通过公路由![]() 到
到![]() 的总运费达到最小值,请确定中转站
的总运费达到最小值,请确定中转站![]() \的位置,并求出
\的位置,并求出![]() 的长.(结果保留根号)
的长.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,![]() 的顶点坐标为:
的顶点坐标为:![]() ,
,![]() ,
,![]() .
.
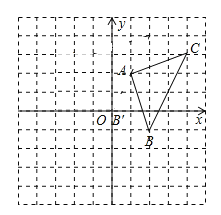
(1)将![]() 向左平移2个单位长度,再向上平移1个单位长度,得
向左平移2个单位长度,再向上平移1个单位长度,得![]() .画出
.画出![]() 并写出
并写出![]() 的顶点坐标;
的顶点坐标;
(2)请判断![]() 的形状并求它的面积.
的形状并求它的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的小正方形组成的![]() 的方格中,
的方格中,![]() 和
和![]() 的顶点都在格点上,且
的顶点都在格点上,且![]() .利用平移、旋转变换,能使
.利用平移、旋转变换,能使![]() 通过一次或两次变换后与
通过一次或两次变换后与![]() 完全重合.
完全重合.

(1)请你写出![]() 通过两次变换与
通过两次变换与![]() 完全重合的变换过程.
完全重合的变换过程.
(2)![]() 通过一次旋转就能得到
通过一次旋转就能得到![]() .请在图中标出旋转中心
.请在图中标出旋转中心![]() ,并简要说明你是如何确定的.
,并简要说明你是如何确定的.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:一次函数的表达式为y=![]() x﹣1
x﹣1
(1)该函数与x轴交点坐标为 ,与y轴的交点坐标为 ;
(2)画出该函数的图象(不必列表);
(3)根据该函数的图象回答下列问题:
①当x 时,则y>0;
②当﹣2≤x<4时,则y的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年宜宾市创建全国文明城市的过程中,某小区决定购买文明用语提示牌和文明信息公示栏.若购买2个提示牌和3个公示栏需要510元;购买3个提示牌和5个公示栏需要840元.
(1)求提示牌和公示栏的单价各是多少元?
(2)若该小区购买提示牌和公示栏共50个,要求购买公示栏至少12个,且总费用不超过3200元.请你列举出所有购买方案,并指出哪种方案费用最少,最少费用为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com