
【题目】已知:一次函数的表达式为y=![]() x﹣1
x﹣1
(1)该函数与x轴交点坐标为 ,与y轴的交点坐标为 ;
(2)画出该函数的图象(不必列表);
(3)根据该函数的图象回答下列问题:
①当x 时,则y>0;
②当﹣2≤x<4时,则y的取值范围是 .
【答案】(1)(2,0),(0,﹣1);(2)详见解析;(3) x>2,﹣2≤y<1
【解析】
(1)把y=0代入y=![]() 得到关于x的一元一次方程,解之,即可得到该函数与x轴交点坐标,把x=0代入y=
得到关于x的一元一次方程,解之,即可得到该函数与x轴交点坐标,把x=0代入y=![]() 得到关于y的一元一次方程,解之,即可得到该函数与y轴交点坐标,
得到关于y的一元一次方程,解之,即可得到该函数与y轴交点坐标,
(2)结合(1)的结果,标出该函数与x轴和y轴的交点,连接两点并延长,即可得到该函数的图象,
(3)由图象可知:该函数的图象上的点y随着x的增大而增大,求出y=0时,x=2;x=﹣2与x=4时y的值,根据图像即可求解.
解:(1)把y=0代入y=![]() 得:
得:![]() ,
,
解得:x=2,
即该函数与x轴交点坐标为(2,0),
把x=0代入y=![]() 得:y=﹣1,
得:y=﹣1,
即该函数与y轴的交点坐标为(0,﹣1),
故答案为:(2,0),(0,﹣1),
(2)标出点(2,0)和点(0,﹣1),连接两点并延长,即可得到该函数的图象,
如下图所示:
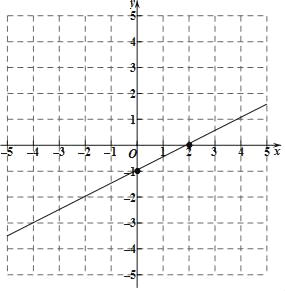
(3)由图象可知:该函数的图象上的点y随着x的增大而增大,
当y=0时,x=2,
即当x>2时,y>0,
把x=﹣2代入y=![]() ﹣1得:y=
﹣1得:y=![]() ×(﹣2)﹣1=﹣2,
×(﹣2)﹣1=﹣2,
把x=4代入y=![]() 得:y=
得:y=![]() ﹣1=1,
﹣1=1,
即当﹣2≤x<4时,y的取值范围是﹣2≤y<1,
故答案为:x>2;﹣2≤y<1.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.

(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
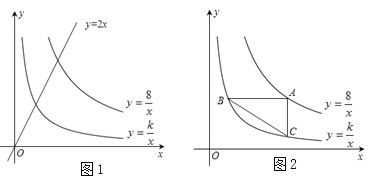
【题目】如图1,已知直线y=2x分别与双曲线![]() ,
, ![]() 交于P、Q(1,n)两点.
交于P、Q(1,n)两点.

(1)求k的值.
(2)如图2,点A是双曲线![]() 上的动点,AB∥x轴,AC∥y轴,分别交双曲线
上的动点,AB∥x轴,AC∥y轴,分别交双曲线![]() 于点B、C,连接BC.试探索在点A运动过程中,△ABC的面积是否变化?若不变,请求出△ABC的面积;若改变,请说明理由;
于点B、C,连接BC.试探索在点A运动过程中,△ABC的面积是否变化?若不变,请求出△ABC的面积;若改变,请说明理由;
(3)如图3,过点B作AC的平行线交直线y=2x于点D,请你进一步探索在点A运动过程中,tan∠ACB=tan∠ADB能否成立?若能,求出此时点A的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB=AE,∠B=∠E,BC=ED,点F是CD的中点,

(1)AC与AD相等吗?为什么?
(2)AF与CD的位置关系如何?说明理由;
(3)若P为AF上的一点,那么PC与PD相等吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△AOB中,AB⊥OB,且AB=OB=3,设直线![]() 截此三角形所得阴影部分的面积为S,则S与t之间的函数关系的图象为下列选项中的( )
截此三角形所得阴影部分的面积为S,则S与t之间的函数关系的图象为下列选项中的( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,对于直线MN同侧的两个点A,B,若直线MN上的点P满足∠APM=∠BPN,则称点P为A,B在直线MN上的反射点.已知如图2,MN∥HG,AP∥BQ,点P为A,B在直线MN上的反射点,判断点B是否为P,Q在直线HG上的反射点,如果是请证明,如果不是,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,Rt△ABC≌Rt△EDF,∠ACB=∠F=90°,∠A=∠E=30°.△EDF绕着边AB的中点D旋转, DE,DF分别交线段AC于点M,K.
(1)观察: ①如图2、图3,当∠CDF=0° 或60°时,AM+CK_______MK(填“>”,“<”或“=”).
②如图4,当∠CDF=30° 时,AM+CK___MK(只填“>”或“<”).
(2)猜想:如图1,当0°<∠CDF<60°时,AM+CK_______MK,证明你所得到的结论.
(3)如果![]() ,请直接写出∠CDF的度数和
,请直接写出∠CDF的度数和![]() 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com