
分析 (1)分a>0,a=0及a<0三种情况进行讨论即可;
(2)根据(1)的结果可得出结论;
(3)先判断出x+1,x-2的符号,再去绝对值符号,合并同类项即可.
解答 解:(1)当a>0时,如a=5,则$\sqrt{{a}^{2}}$=$\sqrt{{5}^{2}}$=5,即$\sqrt{{a}^{2}}$=a;
当a=0 时,$\sqrt{{a}^{2}}$=$\sqrt{0}$=0,即$\sqrt{{a}^{2}}$=0;
当a<0时,如a=-5,则$\sqrt{{a}^{2}}$=$\sqrt{(-5)^{2}}$=5,即$\sqrt{{a}^{2}}$=-a.
综合起来:$\sqrt{{a}^{2}}$=$\left\{\begin{array}{l}{a(a>0)}\\{0(a=0)}\\{-a(a<0)}\end{array}\right.$;
(2)由(1)可知$\sqrt{{a}^{2}}$=|a|;
(3)∵1<x<2,
∴x+1>0,x-2<0,
∴|x+1|+$\sqrt{(x-2)^{2}}$
=|x+1|+|x-2|
=x+1-(x-2)
=3.
点评 本题考查的是二次根式的性质与化简,在解答此题时要注意进行分类讨论,不要漏解.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
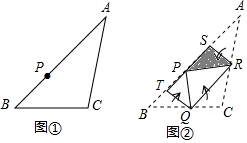 图①为三角形纸片ABC,AB上有一点P,已知将A、B、C往内折至P时,出现折线SR、TQ、QR,其中Q、R、S、T四点分别在BC、AC、AP、BP上,如图②所示,若△ABC、四边形PTQR的面积分别为20、8,则阴影部分面积为( )
图①为三角形纸片ABC,AB上有一点P,已知将A、B、C往内折至P时,出现折线SR、TQ、QR,其中Q、R、S、T四点分别在BC、AC、AP、BP上,如图②所示,若△ABC、四边形PTQR的面积分别为20、8,则阴影部分面积为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
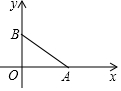 如图,已知:如图点A(4,0),点B在y轴正半轴上,且AB=5,将线段BA绕点A沿顺时针旋转90°,设点B旋转后的对应点是点B1,求点B1的坐标.
如图,已知:如图点A(4,0),点B在y轴正半轴上,且AB=5,将线段BA绕点A沿顺时针旋转90°,设点B旋转后的对应点是点B1,求点B1的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小敏在作⊙O的内接正五边形时.先做了如下几个步骤:
小敏在作⊙O的内接正五边形时.先做了如下几个步骤:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
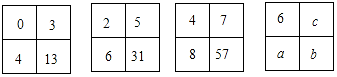
| A. | 10、91 | B. | 12、91 | C. | 10、95 | D. | 12、95 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com