
ЁОЬтФПЁПЕцЧђЪЧХХЧђЖгГЃЙцбЕСЗЕФживЊЯюФПжЎвЛЃЎЯТСаЭМБэжаЕФЪ§ОнЪЧМзЁЂввЁЂБћШ§ШЫУПШЫЪЎДЮЕцЧђВтЪдЕФГЩМЈЃЎВтЪдЙцдђЮЊСЌајНгЧђ10ИіЃЌУПЕцЧђЕНЮЛ1ИіМЧ1ЗжЃЎ
дЫЖЏдБМзВтЪдГЩМЈБэ
ВтЪдађКХ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
ГЩМЈЃЈЗжЃЉ | 7 | 6 | 8 | 7 | 7 | 5 | 8 | 7 | 8 | 7 |

ЃЈ1ЃЉаДГідЫЖЏдБМзВтЪдГЩМЈЕФжкЪ§КЭжаЮЛЪ§ЃЛ
ЃЈ2ЃЉдкЫћУЧШ§ШЫжабЁдёвЛЮЛЕцЧђГЩМЈгХауЧвНЯЮЊЮШЖЈЕФНгЧђФмЪжзїЮЊздгЩШЫЃЌФуШЯЮЊбЁЫИќКЯЪЪ?ЮЊЪВУД? (ВЮПМЪ§ОнЃКШ§ШЫГЩМЈЕФЗНВюЗжБ№ЮЊ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() )
)
ЃЈ3ЃЉМзЁЂввЁЂБћШ§ШЫЯрЛЅжЎМфНјааЕцЧђСЗЯАЃЌУПИіШЫЕФЧђЖМЕШПЩФмЕФДЋИјЦфЫћСНШЫЃЌЧђзюЯШДгМзЪжжаДЋГіЃЌЕкШ§ТжНсЪјЪБЧђЛиЕНМзЪжжаЕФИХТЪЪЧЖрЩйЃПЃЈгУЪїзДЭМЛђСаБэЗЈНтД№ЃЉ
ЁОД№АИЁПЃЈ1ЃЉ7ЃЛ7ЃЈ2ЃЉбЁввдЫЖЏдБИќКЯЪЪЃЈ3ЃЉ![]()
ЁОНтЮіЁП
ЪдЬтЗжЮіЃКЃЈ1ЃЉЙлВьБэИёПЩжЊМздЫЖЏдБВтЪдГЩМЈЕФжкЪ§КЭжаЮЛЪ§ЖМЪЧЃЈ7ЗжЃЉЃЛ
ЃЈ2ЃЉвзжЊ![]() =7ЃЈЗжЃЉЃЌ
=7ЃЈЗжЃЉЃЌ![]() =7ЃЈЗжЃЉЃЌ
=7ЃЈЗжЃЉЃЌ![]() =6.3ЃЈЗжЃЉЃЌИљОнЬтвтВЛФбХаЖЯЃЛ
=6.3ЃЈЗжЃЉЃЌИљОнЬтвтВЛФбХаЖЯЃЛ
ЃЈ3ЃЉЛГіЪїзДЭМЃЌМДПЩНтОіЮЪЬтЃЛ
ЪдЬтНтЮіЃКЃЈ1ЃЉМздЫЖЏдБВтЪдГЩМЈЕФжкЪ§КЭжаЮЛЪ§ЖМЪЧЃЈ7ЗжЃЉЃЎ
ЃЈ2ЃЉЁп![]() =7ЃЈЗжЃЉЃЌ
=7ЃЈЗжЃЉЃЌ![]() =7ЃЈЗжЃЉЃЌ
=7ЃЈЗжЃЉЃЌ![]() =6.3ЃЈЗжЃЉЃЌ
=6.3ЃЈЗжЃЉЃЌ
Ёр![]() =
=![]() ЃО
ЃО![]() ЃЌ
ЃЌ![]() ЃО
ЃО![]()
ЁрбЁввдЫЖЏдБИќКЯЪЪЃЎ
ЃЈ3ЃЉЪїзДЭМШчЭМЫљЪОЃЌ
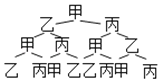
ЕкШ§ТжНсЪјЪБЧђЛиЕНМзЪжжаЕФИХТЪЪЧPЃЈЧѓЛиЕНМзЪжжаЃЉ=![]() ЃЎ
ЃЎ


 УЯНЈЦНаЁбЇЙіЖЏВтЪдЯЕСаД№АИ
УЯНЈЦНаЁбЇЙіЖЏВтЪдЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫНтФГЪаЪаУёЁАТЬЩЋГіааЁБЗНЪНЕФЧщПіЃЌФГаЃЪ§бЇаЫШЄаЁзщвдЮЪОэЕїВщЕФаЮЪНЃЌЫцЛњЕїВщСЫФГЪаВПЗжГіааЪаУёЕФжївЊГіааЗНЪНЃЈВЮгыЮЪОэЕїВщЕФЪаУёЖМжЛДгвдЯТЮхИіжжРржабЁдёвЛРрЃЉЃЌВЂНЋЕїВщНсЙћЛцжЦГЩШчЯТВЛЭъећЕФЭГМЦЭМЃЎ
жжРр | A | B | C | D | E |
ГіааЗНЪН | ЙВЯэЕЅГЕ | ВНаа | ЙЋНЛГЕ | ЕФЪП | ЫНМвГЕ |
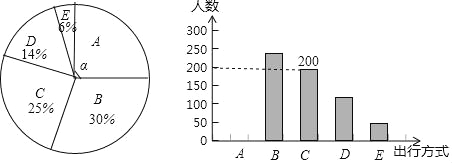
ИљОнвдЩЯаХЯЂЃЌЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉВЮгыБОДЮЮЪОэЕїВщЕФЪаУёЙВга ШЫЃЌЦфжабЁдёBРрЕФШЫЪ§га ШЫЃЛ
ЃЈ2ЃЉдкЩШаЮЭГМЦЭМжаЃЌЧѓAРрЖдгІЩШаЮдВаФНЧІСЕФЖШЪ§ЃЌВЂВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ3ЃЉИУЪадМга12ЭђШЫГіааЃЌШєНЋAЃЌBЃЌCетШ§РрГіааЗНЪНОљЪгЮЊЁАТЬЩЋГіааЁБЗНЪНЃЌЧыЙРМЦИУЪаЁАТЬЩЋГіааЁБЗНЪНЕФШЫЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПBMЪЧЁїABCжаACБпЩЯЕФжаЯпЃЌAB=5cmЃЌBC=3cmЃЌФЧУДЁїABMгыЁїBCMЕФжмГЄжЎВюЮЊ___cmЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§y=Љx2+bx+c+1ЃЌ
ЂйЕБb=1ЪБЃЌЧѓетИіЖўДЮКЏЪ§ЕФЖдГЦжсЕФЗНГЬЃЛ
ЂкШєc=![]() b2Љ2bЃЌЮЪЃКbЮЊКЮжЕЪБЃЌЖўДЮКЏЪ§ЕФЭМЯѓгыxжсЯрЧаЃП
b2Љ2bЃЌЮЪЃКbЮЊКЮжЕЪБЃЌЖўДЮКЏЪ§ЕФЭМЯѓгыxжсЯрЧаЃП
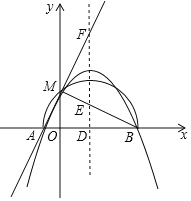
ЂлШєЖўДЮКЏЪ§ЕФЭМЯѓгыxжсНЛгкЕуAЃЈx1ЃЌ0ЃЉЃЌBЃЈx2ЃЌ0ЃЉЃЌЧвx1ЃМx2ЃЌгыyжсЕФе§АыжсНЛгкЕуMЃЌвдABЮЊжБОЖЕФАыдВЧЁКУЙ§ЕуMЃЌЖўДЮКЏЪ§ЕФЖдГЦжсlгыxжсЁЂжБЯпBMЁЂжБЯпAMЗжБ№НЛгкЕуDЁЂEЁЂFЃЌЧвТњзу![]() ЃЌЧѓЖўДЮКЏЪ§ЕФБэДяЪНЃЎ
ЃЌЧѓЖўДЮКЏЪ§ЕФБэДяЪНЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдквдЯТвЛСаЪ§3ЃЌ3ЃЌ5ЃЌ6ЃЌ7ЃЌ8жаЃЌжаЮЛЪ§ЪЧЃЈ ЃЉ
A.3
B.5
C.5.5
D.6
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЛЏМђЃК
ЃЈ1ЃЉЉЃЈa2ЉbЃЉ2+ЃЈ2a+bЃЉЃЈЉ2a+bЃЉЃЛ
ЃЈ2ЃЉ![]() ЁТЃЈmЉ1Љ
ЁТЃЈmЉ1Љ ![]() ЃЉЃЎ
ЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМЦЫу3a3ЃЈЉ2aЃЉ2ЕФНсЙћЪЧЃЈЁЁЁЁЃЉ
A.12a5
B.Љ12a5
C.12a6
D.Љ12a6
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСЃКФмЙЛГЩЮЊжБНЧШ§НЧаЮШ§ЬѕБпГЄЕФШ§Иіе§ећЪ§![]() ЃЌГЦЮЊЙДЙЩЪ§.ЪРНчЩЯЕквЛДЮИјГіЙДЙЩЪ§ЭЈНтЙЋЪНЕФЪЧЮвЙњЙХДњЪ§бЇжјзїЁЖОХеТЫуЪѕЁЗЃЌЦфЙДЙЩЪ§зщЙЋЪНЮЊЃК
ЃЌГЦЮЊЙДЙЩЪ§.ЪРНчЩЯЕквЛДЮИјГіЙДЙЩЪ§ЭЈНтЙЋЪНЕФЪЧЮвЙњЙХДњЪ§бЇжјзїЁЖОХеТЫуЪѕЁЗЃЌЦфЙДЙЩЪ§зщЙЋЪНЮЊЃК
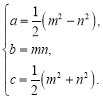 Цфжа
Цфжа![]() ЃЌ
ЃЌ![]() ЪЧЛЅжЪЕФЦцЪ§.
ЪЧЛЅжЪЕФЦцЪ§.
гІгУЃЌЕБ![]() ЪБЃЌЧѓгавЛБпГЄЮЊ5ЕФжБНЧШ§НЧаЮЕФСэЭтСНЬѕБпГЄ.
ЪБЃЌЧѓгавЛБпГЄЮЊ5ЕФжБНЧШ§НЧаЮЕФСэЭтСНЬѕБпГЄ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊABЮЊЁбOЕФжБОЖЃЌBCЁЭABгкBЃЌЧвBC=ABЃЌDЮЊАыдВЁбOЩЯЕФвЛЕуЃЌСЌНгBDВЂбгГЄНЛАыдВЁбOЕФЧаЯпAEгкEЃЎ
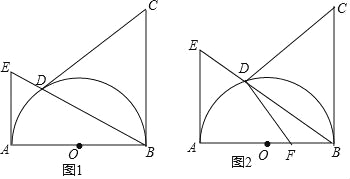
ЃЈ1ЃЉШчЭМ1ЃЌШєCD=CBЃЌЧѓжЄЃКCDЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌШєFЕудкOBЩЯЃЌЧвCDЁЭDFЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com