
【题目】化简:
(1)﹣(a2﹣b)2+(2a+b)(﹣2a+b);
(2)![]() ÷(m﹣1﹣
÷(m﹣1﹣ ![]() ).
).
【答案】
(1)解:﹣(a2﹣b)2+(2a+b)(﹣2a+b)
=﹣a4+2a2b﹣b2+b2﹣4a2
=﹣a4+2a2b﹣4a2
(2)解: ![]() ÷(m﹣1﹣
÷(m﹣1﹣ ![]() )
)
= ![]()
= ![]()
= ![]()
【解析】(1)根据完全平公式和平方差公式将原式展开,然后合并同类项即可解答本题;(2)先化简括号内的式子,然后根据分式的除法可以化简本题.
【考点精析】利用分式的混合运算和完全平方公式对题目进行判断即可得到答案,需要熟知运算的顺序:第一级运算是加法和减法;第二级运算是乘法和除法;第三级运算是乘方.如果一个式子里含有几级运算,那么先做第三级运算,再作第二级运算,最后再做第一级运算;如果有括号先做括号里面的运算.如顺口溜:"先三后二再做一,有了括号先做里."当有多层括号时,先算括号内的运算,从里向外{[(?)]};首平方又末平方,二倍首末在中央.和的平方加再加,先减后加差平方.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:
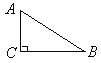
【题目】如图,![]() 那么点A到BC的距离是_____,点B到AC的距离是_______,点A、B两点的距离是_____,点C到AB的距离是________.
那么点A到BC的距离是_____,点B到AC的距离是_______,点A、B两点的距离是_____,点C到AB的距离是________.
设![]() 、b、c为平面上三条不同直线,
、b、c为平面上三条不同直线,
①若![]() ,则a与c的位置关系是_________;
,则a与c的位置关系是_________;
②若![]() ,则a与c的位置关系是________;
,则a与c的位置关系是________;
③若![]() ,
,![]() ,则a与c的位置关系是________.
,则a与c的位置关系是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一些书分给几名同学,若每人分11本,则有剩余,若( ),依题意,设有x名同学,可列不等式7(x+4)>11x.
A.每人分7本,则剩余4本
B.每人分7本,则剩余的书可多分给4个人
C.每人分4本,则剩余7本
D.其中一个人分7本,则其他同学每人可分4本
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】垫球是排球队常规训练的重要项目之一.下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩.测试规则为连续接球10个,每垫球到位1个记1分.
运动员甲测试成绩表
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩(分) | 7 | 6 | 8 | 7 | 7 | 5 | 8 | 7 | 8 | 7 |

(1)写出运动员甲测试成绩的众数和中位数;
(2)在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?为什么? (参考数据:三人成绩的方差分别为![]() 、
、![]() 、
、![]() )
)
(3)甲、乙、丙三人相互之间进行垫球练习,每个人的球都等可能的传给其他两人,球最先从甲手中传出,第三轮结束时球回到甲手中的概率是多少?(用树状图或列表法解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2). 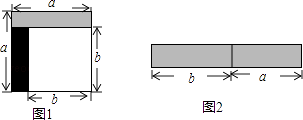
(1)上述操作能验证的等式是(填A或B)
A.a2﹣2ab+b2=(a﹣b)2
B.a2﹣b2=(a+b)(a﹣b)
(2)应用你从(1)中选出的等式,计算: (1﹣ ![]() )(1﹣
)(1﹣ ![]() )(1﹣
)(1﹣ ![]() )…(1﹣
)…(1﹣ ![]() )(1﹣
)(1﹣ ![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
问题:某饭店工作人员第一次买了13只鸡、5只鸭、9只鹅共用了925元.第二次买了2只鸡、4只鸭、3只鹅共用了320元,试问第三次买了鸡、鸭、鹅各一只共需多少元?(假定三次购买鸡、鸭、鹅的单价不变)
解:设鸡、鸭、鹅的单价分别为x,y,z元.依题意,得![]()
上述方程组可变形为![]()
设x+y+z=a,2x+z=b,上述方程组可化为:![]()
①+4×②得:a=____,即x+y+z=____.
答:第三次买鸡、鸭、鹅各一只共需____元.
阅读后,细心的你,可以解决下列问题:(1)上述材料中a= ;
(2)选择题:上述材料中的解答过程运用了 思想方法来指导解题.
A.整体 B.数形结合 C.分类讨论
(3)某校体育组购买体育用品甲、乙、丙、丁的件数和用钱金额如下表:
品名 次数 | 甲 | 乙 | 丙 | 丁 | 用钱金额(元) |
第一次购买件数 | 5 | 4 | 3 | 1 | 1 882 |
第二次购买件数 | 9 | 7 | 5 | 1 | 2 764 |
那么购买每种体育用品各一件共需多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知y=3x+3与x轴交于点B,与y轴交于点A,与函数y=x的图象交于点P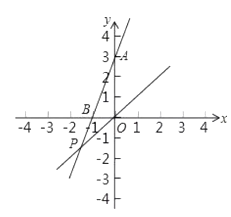
(1)在该坐标系中画出函数y= ![]()
![]() 的图象,并说明点P也在函数y=
的图象,并说明点P也在函数y= ![]()
![]() 的图象上;
的图象上;
(2)设直线y= ![]() 与x轴交于点C,与y轴交于点D,求证:PO平分∠APC;
与x轴交于点C,与y轴交于点D,求证:PO平分∠APC;
(3)连接AC,求△APC的面积;
(4)在y轴上,是否存在点M,使△ACM为等腰三角形?若存在,请直接写出符合条件的所有点M的坐标;若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com