
【题目】如图,已知y=3x+3与x轴交于点B,与y轴交于点A,与函数y=x的图象交于点P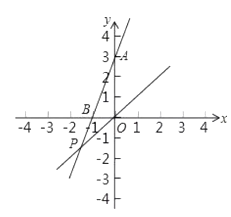
(1)在该坐标系中画出函数y= ![]()
![]() 的图象,并说明点P也在函数y=
的图象,并说明点P也在函数y= ![]()
![]() 的图象上;
的图象上;
(2)设直线y= ![]() 与x轴交于点C,与y轴交于点D,求证:PO平分∠APC;
与x轴交于点C,与y轴交于点D,求证:PO平分∠APC;
(3)连接AC,求△APC的面积;
(4)在y轴上,是否存在点M,使△ACM为等腰三角形?若存在,请直接写出符合条件的所有点M的坐标;若不存在,请说明理由。
【答案】
(1)解:如图,解方程组,得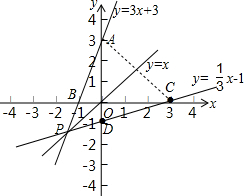
|
得
|
,
则P点坐标为(-
3 |
2 |
,-
3 |
2 |
),
当x=-
3 |
2 |
时,y=
1 |
3 |
x(![]() -1=
-1=
1 |
3 |
×(-
3 |
2 |
)-1=-
3 |
2 |
,所以点P在函数y=![]() x-1
x-1
的图象上 |
(2)证明:∵点A(0,3)和点C(3,0)关于直线y=x对称,
∴直线y=x垂直平分AC,
∴PO平分∠APC;
(3)解:B(-1,0),A(0,3),
△APC的面积=S△ABC+S△PBC
= ![]() ×(3+1)×3+
×(3+1)×3+ ![]() ×(3+1)×3=9.
×(3+1)×3=9.
(4)AC=![]() ,
,
当AC=AM时,OM=AM-OA=![]() -3,M坐标为(0,3-
-3,M坐标为(0,3-![]() )或(0,3+
)或(0,3+![]() );
);
当CA=CM时,OA=OM=3,M坐标为(0.-3);
当MA=MC时,M在原点,坐标为(0,0)
【解析】
(1)两直线相交或平行:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解;若两条直线是平行的关系,那么他们的自变量系数相同,即k值相同,由此可进行求解.(2)可证明PO所在三角形为等腰三角形,即直线y=x垂直平分AC,可得到平分顶角;(4)等腰三角形需分为三类,A、C、M分别为顶角顶点,由等腰三角形的性质可求出M坐标.


科目:初中数学 来源: 题型:
【题目】若(8×106)(5×102)(2×10)=M×10a , 则M、a的值为( )
A.M=8,a=8
B.M=2,a=9
C.M=8,a=10
D.M=5,a=10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读:能够成为直角三角形三条边长的三个正整数![]() ,称为勾股数.世界上第一次给出勾股数通解公式的是我国古代数学著作《九章算术》,其勾股数组公式为:
,称为勾股数.世界上第一次给出勾股数通解公式的是我国古代数学著作《九章算术》,其勾股数组公式为:
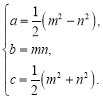 其中
其中![]() ,
,![]() 是互质的奇数.
是互质的奇数.
应用,当![]() 时,求有一边长为5的直角三角形的另外两条边长.
时,求有一边长为5的直角三角形的另外两条边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是甲、乙、丙三人百米赛跑的函数图象,根据右图回答下面问题;
(1)在这次比赛中,获得冠军:
(2)甲比乙提前秒到达目的地;
(3)乙的速度比丙快米/秒.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】庆祝新中国成立70周年,国庆假期期间,各旅游景区节庆氛围浓厚,某景区同步设置的“我为祖国点赞”装置共收集约6390000个“赞”,这个数字用科学记数法可表示为( )
A.6.39×106B.0.639×106C.0.639×105D.6.39×105
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com