
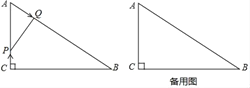
【题目】如图,已知Rt△ABC中,∠C=90°,∠A=60°,AC=3cm,AB=6m,点P在线段AC上以1cm/s的速度由点C向点A运动,同时,点Q在线段AB上以2cm/s的速度由点A向点B运动,设运动时间为t(s).
(1)当t=1时,判断△APQ的形状,并说明理由;
(2)当t为何值时,△APQ与△CQP全等?请写出证明过程.
【答案】(1)△APQ是等边三角形;(2)t=1.5.
【解析】
(1)分别求出AP、AQ的长,根据等边三角形的判定定理即可得出结论;
(2)根据全等的条件和已知分别求出AP、CP、AQ、CQ的长,根据全等三角形的判定定理即可得出结论.
(1)△APQ是等边三角形.理由如下:
∵t=1,∴AP=3﹣1×1=2,AQ=2×1=2,∴AP=AQ.
∵∠A=60°,∴△APQ是等边三角形;
(2)存在t,使△APQ和△CPQ全等.当t=1.5s时,△APQ和△CPQ全等.理由如下:∵在Rt△ACB中,AB=6,AC=3,∴∠B=30°,∠A=60°,当t=1.5时,此时AP=PC.
∵t=1.5s,∴AP=CP=1.5cm.
∵AQ=3cm,∴AQ=AC.
又∵∠A=60°,∴△ACQ是等边三角形,∴AQ=CQ.
在△APQ和△CPQ中,∵AQ=CQ,AP=CP,PQ=PQ,∴△APQ≌△CPQ(SSS);
即存在时间t,使△APQ和△CPQ全等,时间t=1.5;


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形OABC和正方形CDEF在平面直角坐标系中,点O,C,F在y轴上,点O为坐标原点,点M为OC的中点,抛物线y=ax2+b经过M,B,E三点,则 ![]() 的值为 .
的值为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正△ABC的边长为2,以BC边上的高AB1为边作正△AB1C1,△ABC与△AB1C1公共部分的面积记为S1;再以正△AB1C1边B1C1上的高AB2为边作正△AB2C2,△AB1C1与△AB2C2公共部分的面积记为S2;…,以此类推,则Sn=____.(用含n的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一块直角三角板ABC中,∠C=90°,∠A=30°,BC=1,将另一个含30°角的△EDF的30°角的顶点D放在AB边上,E,F分别在AC,BC上,当点D在AB边上移动时,DE始终与AB垂直,若△CEF与△DEF相似,则AD= . 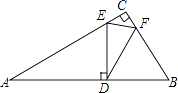
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,∠BOM=90°,∠DON=90°.
(1)若∠COM=∠AOC,求∠AOD的度数;
(2)若∠COM=![]() ∠BOC,求∠AOC和∠MOD.
∠BOC,求∠AOC和∠MOD.

查看答案和解析>>
科目:初中数学 来源: 题型:
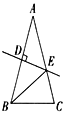
【题目】如图,等腰三角形ABC的底角为72°,腰AB的垂直平分线交另一腰AC于点E,垂足为D,连接BE,则下列结论错误的是( )
A. ∠EBC为36° B. BC = AE
C. 图中有2个等腰三角形 D. DE平分∠AEB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点A,B,C在同一条直线上,点M、N分别是AB、AC的中点,如果AB=10cm,AC=8cm,那么线段MN的长度为( )
A. 6cm B. 9cm C. 3cm或6cm D. 1cm或9cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的度数;
(2)若CD=2,求DF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校共有900名学生,学校准备调查他们对“沈阳创建卫生城”知识的了解程度,团委对部分学生采用了随机抽样调查的方式,并用收集到的数据绘制出两幅不完整的统计图(如图①、图②所示):

(1)根据图中信息,学校决定对“不了解”和“了解一点”的同学进行培训,估计该校约有多少名学生参加培训?
(2)请你直接将两个统计图补充完整.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com