
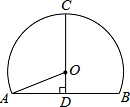
 如图是一个单心圆隧道的截面,若路面AB宽为10m,高CD为7m,则此隧道单心圆的半径OA是$\frac{37}{7}$m.
如图是一个单心圆隧道的截面,若路面AB宽为10m,高CD为7m,则此隧道单心圆的半径OA是$\frac{37}{7}$m. 分析 因为CD为高,根据垂径定理,CD平分AB,则AD=BD=5,在Rt△AOD中,有OA2=AD2+OD2,进而可求得半径OA.
解答 解:因为CD为高,
根据垂径定理:CD平分AB,
又路面AB宽为10m
则有:AD=$\frac{1}{2}$AB=5m,
设圆的半径是x米,
在Rt△AOD中,有OA2=AD2+OD2,
即:x2=52+(7-x)2,
解得:x=$\frac{37}{7}$,
所以圆的半径长是$\frac{37}{7}$m.
故答案为$\frac{37}{7}$m.
点评 本题考查了垂径定理的应用和勾股定理的应用,解决与弦有关的问题时,往往需构造以半径、弦心距和弦长的一半为三边的直角三角形,若设圆的半径为r,弦长为a,这条弦的弦心距为d,则有等式r2=d2+($\frac{a}{2}$)2成立,知道这三个量中的任意两个,就可以求出另外一个.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:填空题
 如果将点P绕定点M旋转180°后与点Q重合,那么点P与点Q关于点M对称,定点M叫做对称中心,此时,点M是线段PQ的中点,如图,在直角坐标系中,△ABO的顶点A、B、O的坐标分别为(1,0),(0,1),(0,0),点列P1、P2、P3…中的相邻两点都关于△ABO的一个顶点对称,点P1与点P2关于点A对称,点P2与点P3关于点B对称,点P3与点P4关于点O对称,点P4与点P5关于点A对称,点P5与点P6关于点B对称,点P6与点P7关于点O对称,且这些对称中心依次循环,已知点P1的坐标是(1,1),则点P2015的坐标为(1,3).
如果将点P绕定点M旋转180°后与点Q重合,那么点P与点Q关于点M对称,定点M叫做对称中心,此时,点M是线段PQ的中点,如图,在直角坐标系中,△ABO的顶点A、B、O的坐标分别为(1,0),(0,1),(0,0),点列P1、P2、P3…中的相邻两点都关于△ABO的一个顶点对称,点P1与点P2关于点A对称,点P2与点P3关于点B对称,点P3与点P4关于点O对称,点P4与点P5关于点A对称,点P5与点P6关于点B对称,点P6与点P7关于点O对称,且这些对称中心依次循环,已知点P1的坐标是(1,1),则点P2015的坐标为(1,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| a | 5 | 4 | -2 | -3 | 2 | |
| b | 3 | 0 | -1 | 0 | -4 | |
| A、B两点间的距离 | 2 | 3 | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com