

 x+6
x+6  =
=
 ,解得
,解得

 ,解得t=
,解得t=
 或t=
或t= 时,以点A、P、Q为顶点的三角形与△AOB相似。
时,以点A、P、Q为顶点的三角形与△AOB相似。 
 =
= ,则QM=4.8
,则QM=4.8

 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源:不详 题型:解答题
 的边长为1,射线
的边长为1,射线 与射线
与射线 交于点
交于点 ,射线
,射线 与射线
与射线 交于点
交于点 ,
, .
.
 在线段
在线段 上时,试猜想线段
上时,试猜想线段 、
、 、
、 有怎样的数量关系?并证明你的猜想.
有怎样的数量关系?并证明你的猜想. ,
, ,当点
,当点 在线段
在线段 上运动时(不包括点
上运动时(不包括点 、
、 ),如图1,求
),如图1,求 关于
关于 的函数解析式,并指出
的函数解析式,并指出 的取值范围.
的取值范围. 在射线
在射线 上运动时(不含端点
上运动时(不含端点 ),点
),点 在射线
在射线 上运动.试判断以
上运动.试判断以 为圆心以
为圆心以 为半径的
为半径的 和以
和以 为圆心以
为圆心以 为半径的
为半径的 之间的位置关系.
之间的位置关系.
 在
在 延长线上时,设
延长线上时,设 与
与 交于点
交于点 ,如图2.问△
,如图2.问△ 与△
与△ 能否相似,若能相似,求出
能否相似,若能相似,求出 的值,若不可能相似,请说明理由.
的值,若不可能相似,请说明理由.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
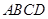 的边长为4,
的边长为4,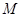 、
、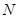 分别是
分别是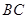 、
、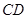 上的两个动点,当
上的两个动点,当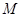 点在
点在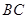 上运动时,始终保持
上运动时,始终保持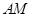 和
和 垂直,
垂直,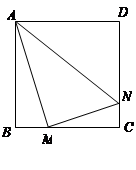
 ;
;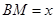 ,梯形
,梯形 的面积为
的面积为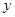 ,求
,求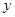 与
与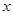 之间的函数关系式;当
之间的函数关系式;当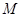 点运动到什么位置时,四边形
点运动到什么位置时,四边形 面积最大,并求出最大面积;
面积最大,并求出最大面积;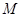 点运动到什么位置时,
点运动到什么位置时, ?并求出此时BM的长.
?并求出此时BM的长.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com