
【题目】如图,在△ABC中,AD⊥BC垂足为点D,AD是BC边上的中线,BE⊥AC,垂足为点E.则以下4个结论:①AB=AC;②∠EBC=![]() ;③AE=CE;④∠EBC=
;③AE=CE;④∠EBC=![]() 中正确的有( )
中正确的有( )

A.①② B.②③ C.①②③ D.①②③④
【答案】A
【解析】
试题分析:根据线段的垂直平分线的性质求出AB=AC,进一步求得∠BAD=∠CAD=![]() ∠BAC;根据等角的余角相等即可求出∠EBC=∠DAC=
∠BAC;根据等角的余角相等即可求出∠EBC=∠DAC=![]() ∠BAC;根据勾股定理即可判断③,根据∠BAC≠∠ABC,∠EBC=
∠BAC;根据勾股定理即可判断③,根据∠BAC≠∠ABC,∠EBC=![]() ∠BAC,即可判断④.
∠BAC,即可判断④.
解:∵AD⊥BC垂足为点D,AD是BC边上的中线,
∴AD垂直平分BC,
∴AB=AC,∴①正确;
∵AB=AC,AD⊥BC,
∴∠BAD=∠CAD=![]() ∠BAC,
∠BAC,
∵BE⊥AC,AD⊥BC,
∴∠EBC+∠C=90°,∠DAC+∠C=90°,
∴∠EBC=∠DAC,
∴∠EBC=![]() ∠BAC,∴②正确;
∠BAC,∴②正确;
∵AE2=AB2﹣BE2,CE2=BC2﹣BE2,AB≠BC,
∴AE≠CE,∴③错误;
∵∠BAC≠∠ABC,∠EBC=![]() ∠BAC,
∠BAC,
∴∠EBC≠![]() ∠ABC,∴④错误;
∠ABC,∴④错误;
∴①②都正确;
故选A.


科目:初中数学 来源: 题型:
【题目】练习本比水性笔的单价少2元,小刚买了5本练习本和3支水性笔正好用去14元. 如果设水性笔的单价为x元,那么下列所列方程正确的是( )
A.5(x-2)+3x=14
B.5(x+2)+3x=14
C.5x+3(x+2)=14
D.5x+3(x-2)=14
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知O是坐标原点,B、C两点的坐标分别为(3,﹣1)、(2,1).
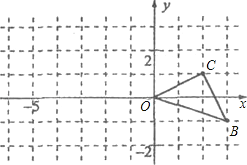
(1)以0点为位似中心在y轴的左侧将△OBC放大到两倍(即新图与原图的相似比为2),画出图形;
(2)分别写出B、C两点的对应点B′、C′的坐标;
(3)如果△OBC内部一点M的坐标为(x,y),写出M的对应点M′的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O直径,OC⊥AB,弦CD与OB交于点F,过点D、A分别作⊙O的切线交于点G,切线GD与AB延长线交于点E.
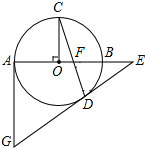
(1)求证:∠C+∠EDF=90°
(2)已知:AG=6,⊙O的半径为3,求OF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小乐的数学积累本上有这样一道题:
解方程:![]() ﹣
﹣![]() =1
=1
解:去分母,得6(2x+1)﹣(5x﹣1)=6…第一步
去括号,得4x+2﹣5x﹣1=6…第二步
移向、合并同类项,得x=5…第三步
方程两边同除以﹣1,得x=﹣5…第四步
在题后的反思中看,小郑总结到:解一元一次方程的一般步骤都知道,却没有掌握好,因此解题时有一步出现了错误…
小乐的解法从第 步开始出现错误,然后,请你自己细心地解下面的方程:
2﹣![]() (x+2)=
(x+2)=![]() (x﹣1)
(x﹣1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com