
【题目】如图,AB是⊙O直径,OC⊥AB,弦CD与OB交于点F,过点D、A分别作⊙O的切线交于点G,切线GD与AB延长线交于点E.
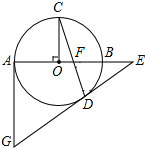
(1)求证:∠C+∠EDF=90°
(2)已知:AG=6,⊙O的半径为3,求OF的值.
【答案】(1)见解析;(2)1
【解析】
试题分析:(1)连接OD,根据切线的性质得OD⊥DE,则∠EDF+∠ODC=90°,而∠C=∠ODC,则∠EDF+∠C=90°.
(2)先求得EF=ED,设DE=x,则EF=x,根据切线的性质由AG为⊙O的切线得∠ODE=90°,再证明Rt△EOD∽Rt△EGA,利用相似比求得AE=2x,OE=3+![]() x,然后根据AE﹣OE=OA=3,求得x的值,进而求得OF=1.
x,然后根据AE﹣OE=OA=3,求得x的值,进而求得OF=1.
(1)证明:连接OD,
∵DE为⊙O的切线,
∴OD⊥DE,
∴∠ODE=90°,即∠EDF+∠ODC=90°,
∵OC=OD,
∴∠C=∠ODC,
∴∠C+∠EDF=90°.
(2)解:∵∠C+∠EDF=90°,∠C+∠CFO=90°,∠CFO=∠EFD,
∴∠EFD=∠EDF,
∴EF=ED,
设DE=x,则EF=x,
∵∠ODE=∠GAE,∠OED=∠GEA,
∴Rt△EOD∽Rt△EGA,
∴![]() =
=![]() =
=![]() ,即
,即![]() =
=![]() =
=![]() ,
,
∴AE=2x,OE=3+![]() x,
x,
∵AE﹣OE=OA=3,
∴2x﹣(3+![]() x)=3,解得x=4,
x)=3,解得x=4,
∴AE=2x=8,
∴OF=AE﹣EF﹣OA=8﹣3﹣4=1.


科目:初中数学 来源: 题型:
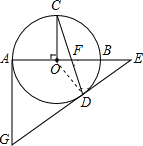
【题目】如图,AB表示路灯,当身高为1.6米的小名站在离路灯1.6的D处时,他测得自己在路灯下的影长DE与身高CD相等,当小明继续沿直线BD往前走到E点时,画出此时小明的影子,并计算此时小明的影长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有四张正面分别标有数字2,1,﹣3,﹣4的不透明卡片,它们除数字外其余全部相同,现将它们背面朝上,洗匀后从四张卡片中随机地摸取一张不放回,将该卡片上的数字记为m,再随机地摸取一张,将卡片上的数字记为n.
(1)请画出树状图并写出(m,n)所有可能的结果;
(2)求所选出的m,n能使一次函数y=mx+n的图象经过第二、三、四象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD⊥BC垂足为点D,AD是BC边上的中线,BE⊥AC,垂足为点E.则以下4个结论:①AB=AC;②∠EBC=![]() ;③AE=CE;④∠EBC=
;③AE=CE;④∠EBC=![]() 中正确的有( )
中正确的有( )

A.①② B.②③ C.①②③ D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程或方程组解应用题:
近年来,我国逐步完善养老金保险制度.甲、乙两人计划用相同的年数分别缴纳养老保险金15万元和10万元,甲计划比乙每年多缴纳养老保险金0.2万元.求甲、乙两人计划每年分别缴纳养老保险金多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】情境观察:
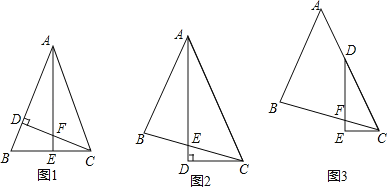
如图1,△ABC中,AB=AC,∠BAC=45°,CD⊥AB,AE⊥BC,垂足分别为D、E,CD与AE交于点F.
①写出图1中所有的全等三角形 ;
②线段AF与线段CE的数量关系是 .
问题探究:
如图2,△ABC中,∠BAC=45°,AB=BC,AD平分∠BAC,AD⊥CD,垂足为D,AD与BC交于点E.
求证:AE=2CD.
拓展延伸:
如图3,△ABC中,∠BAC=45°,AB=BC,点D在AC上,∠EDC=![]() ∠BAC,DE⊥CE,垂足为E,DE与BC交于点F.求证:DF=2CE.
∠BAC,DE⊥CE,垂足为E,DE与BC交于点F.求证:DF=2CE.
要求:请你写出辅助线的作法,并在图3中画出辅助线,不需要证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD中,∠DAB=∠B=∠C=∠D=90°,AD=BC=8,AB=CD=17.点E为射线DC上的一个动点,△ADE与△AD′E关于直线AE对称,当△AD′B为直角三角形时,DE的长为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com