
【题目】如图,矩形ABCD中,P为AD上一点,将△ABP沿BP翻折至△EBP,点A与点E重合;
(1)如图1,若AB=10,BC=6,点E落在CD边上,求AP的长;
(2)如图2,若AB=8,BC=6, PE与CD相交于点O,且OE=OD,求AP的长;
(3)如图3,若AB=4,BC=6,点P是AD的中点,求DE的长.

【答案】(1)![]() (2)4.8(3)3.6
(2)4.8(3)3.6
【解析】试题分析:(1)在Rt△BCE中,BC=6,BE=AB=10,根据勾股定理求出CE的值为8,则DE=10-8=2,设AP=x,则PE=x,DP=6-x,在Rt△DPE中,根据勾股定理得出方程,解方程即可;
(2)由折叠的性质得出EP=AP,∠E=∠A=90°,BE=AB=8,由ASA证明△ODP≌△OEG,得出OP=OG,PD=GE,设AP=EP=x,则PD=GE=6-x,DG=x,求出CG、BG,根据勾股定理得出方程,解方程即可;
(3)以点A为原点建立平面直角坐标系,则点A(0,0),B(4,0),C(4,6),D(0,6),P(0,3),设点E的坐标为(x,y),根据PE=PA=3可得,PE=![]() ,BE=
,BE=![]() ,解得y=
,解得y= ![]() ,再将y=
,再将y= ![]() 代入
代入![]() 中得,x(
中得,x(![]() )=0,所以x=0或x=
)=0,所以x=0或x=![]() ,所以y=
,所以y=![]() ,再根据DE=
,再根据DE=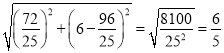 ;
;
试题解析:
(1)∵△ABP沿BP翻折至△EBP,点A与点E重合,AB=10,
∴BE=AB=10,PE=AP,
∴在Rt△BCE中,CE=![]() ,
,
∴DE=CD-CE=2,
设AP=x,则DP=6-x
∵在Rt△DPE中,DP2+DE2=PE2,
∴(6-x)2+22=x2,
∴x=![]() ;
;
(2)∵四边形ABCD是矩形,
∴∠D=∠A=∠C=90°,AD=BC=6,CD=AB=8,
根据题意得:△ABP≌△EBP,
∴EP=AP,∠E=∠A=90°,BE=AB=8,
在△ODP和△OEG中,
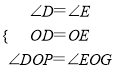
∴△ODP≌△OEG(ASA),
∴OP=OG,PD=GE,
∴DG=EP,
设AP=EP=x,则PD=GE=6-x,DG=x,
∴CG=8-x,BG=8-(6-x)=2+x,
根据勾股定理得:BC2+CG2=BG2,
即62+(8-x)2=(x+2)2,
解得:x=4.8,
∴AP=4.8;
(3)以点A为原点建立平面直角坐标系,则点A(0,0),B(4,0),C(4,6),D(0,6),P(0,3),设点E的坐标为(x,y),根据PE=PA=3可得,
PE=![]() ,BE=
,BE=![]() ,
,
解得y= ![]() ,
,
把y= ![]() 代入
代入![]() 中得,
中得,
x(![]() )=0,
)=0,
所以x=0(舍去)或x=![]() ,
,
所以y=![]() ,
,
∴DE=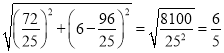 ;
;


科目:初中数学 来源: 题型:
【题目】如图,己知△ABC中,∠C=90°,∠A=30°,AC=![]() .动点D在边AC上,以BD为边作等边△BDE(点E、A在BD的同侧).在点D从点A移动至点C的过程中,点E移动的路线长为 .
.动点D在边AC上,以BD为边作等边△BDE(点E、A在BD的同侧).在点D从点A移动至点C的过程中,点E移动的路线长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校国旗护卫队成员的身高分布加下表:
身高/cm | 159 | 160 | 161 | 162 |
人数 | 7 | 10 | 9 | 9 |
则学校国旗护卫队成员的身高的众数和中位数分别是( )
A.160和160B.160和160.5C.160和161D.161和161
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从泰州到某市,可乘坐普通列车或动车,已知动车的行驶路程是400千米,普通列车的行驶路程是动车的行驶路程的1.3倍.
(1)求普通列车的行驶路程;
(2)若动车的平均速度(千米/时)是普通列车平均速度(千米/时)的2.5倍,且乘坐动车所需时间比乘坐普通列车所需时间缩短3小时,求动车的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级一班数学老师对全班学生在模拟考试中A卷成绩进行统计后,制成如下的统计表:
成绩(分) | 80 | 82 | 84 | 86 | 87 | 90 |
人数 | 8 | 12 | 9 | 3 | 5 | 8 |
则该班学生A卷成绩的众数和中位数分别是( )
A. 82分,82分 B. 82分,83分 C. 80分,82分 D. 82分,84分
查看答案和解析>>
科目:初中数学 来源: 题型:
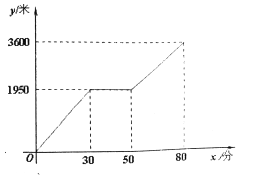
【题目】小颖和小亮上山游玩,小颗乘坐缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍,小颗在小亮出发后50分才乘上缆车,缆车的平均速度为180米/分,设小亮出发x分后行走的路程为y米。图中的折线表示小亮在整个行走过程中y随x的变化关系.
(1)小亮行走的总路程是_________米,他途中休息了___________分;
(2)分别求出小亮在休息前和休息后所走的路程段上的步行速度;
(3)当小颖到达缆车终点时,小亮离缆车终点的路程是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是等腰△ABC底边BC上的高.点O是AC中点,延长DO到E,使OE=OD,连接AE,CE.
(1)求证:四边形ADCE的是矩形;
(2)若AB=17,BC=16,求四边形ADCE的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com