
【题目】如图,AD是等腰△ABC底边BC上的高.点O是AC中点,延长DO到E,使OE=OD,连接AE,CE.
(1)求证:四边形ADCE的是矩形;
(2)若AB=17,BC=16,求四边形ADCE的面积.

【答案】6.
【解析】(1)根据平行四边形的性质得出四边形ABCD是平行四边形,根据垂直推出∠ADC=90°,根据矩形的判定得出即可;
(2)求出DC,根据勾股定理求出AD,根据矩形的面积公式求出即可.
解:(1)证明:∵点O是AC的中点,
∴AO=OC,
∵OE=OD,
∴四边形ADCE是平行四边形,
∵AD是等腰△ABC底边上的高,
∴∠ADC=90°,
∴四边形ADCE是矩形.
(2)∵AD是等腰△ABC底边上的高,BC=16,AB=17,
∴BD=CD=8,AB=AC=17,∠ADC=90°,
由勾股定理得:AD=![]() =
=![]() =15,
=15,
∴四边形ADCE的面积是AD×DC=15×8=120.
“点睛”本题考查了平行四边形的判定,矩形的判定和性质,等腰三角形的性质,勾股定理的应用,能综合运用定理进行推理和计算是解此题的关键.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,P为AD上一点,将△ABP沿BP翻折至△EBP,点A与点E重合;
(1)如图1,若AB=10,BC=6,点E落在CD边上,求AP的长;
(2)如图2,若AB=8,BC=6, PE与CD相交于点O,且OE=OD,求AP的长;
(3)如图3,若AB=4,BC=6,点P是AD的中点,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分6分)
(1)(3分)(-3)2-|-![]() |+(3.14-x)0
|+(3.14-x)0
(2)(4分)先化简,再求值:[(2x-y)2+(2x-y)(2x+y)]÷(4x),其中x=2,y=-1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】适合下列条件的△ABC中,直角三角形的个数为( )
①a=![]() ,b=
,b=![]() ,c=
,c=![]() ②a=6,∠A=45°; ③∠A=32°,∠B=58°;
②a=6,∠A=45°; ③∠A=32°,∠B=58°;
④a=7,b=24,c=25 ⑤a=2,b=2,c=4.
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大型企业为了保护环境,准备购买A、B两种型号的污水处理设备共8台,用于同时治理不同成分的污水,若购买A型2台、B型3台需54万,购买A型4台、B型2台需68万元.
(1)求出A型、B型污水处理设备的单价;
(2)经核实,一台A型设备一个月可处理污水220吨,一台B型设备一个月可处理污水190吨,如果该企业每月的污水处理量不低于1565吨,请你为该企业设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列数据中不能确定物体位置的是( )
A. 某市政府位于北京路32号 B. 小明住在某小区3号楼7号
C. 太阳在我们的正上方 D. 东经130°,北纬54°的城市
查看答案和解析>>
科目:初中数学 来源: 题型:
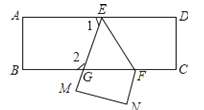
【题目】把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G、D、C分别在M、N的位置上,若∠EFG=55°,则∠1=______°,∠2=_______°.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com