
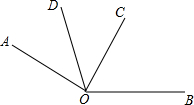
 如下图,∠AOC是直角,OD平分∠AOC,∠BOC=60° 求:
如下图,∠AOC是直角,OD平分∠AOC,∠BOC=60° 求:分析 (1)根据∠AOC是直角,OD平分∠AOC及角平分线的定义,解答即可;
(2)根据图形,通过∠AOC与∠BOC的和,即可解答;
(3)根据角平分线的定义,求出∠DOC,根据∠DOC与∠BOC的和,即可解答.
解答 解:(1)∵∠AOC是直角,OD平分∠AOC,
∴∠AOD=$\frac{1}{2}$∠AOC=$\frac{1}{2}$×90°=45°;
(2)∵∠AOC=90°,∠BOC=60°,
∴∠AOB=∠AOC+∠BOC=90°+60°=150°;
(3))∵∠AOC是直角,OD平分∠AOC,
∴∠COD=$\frac{1}{2}$∠AOC=$\frac{1}{2}$×90°=45°,
∵∠BOC=60°,
∴∠DOB=∠DOC+∠COB=45°+60°=105°.
点评 本题主要考查角的和差,根据图形找出是哪几个角的和是解决此题的关键.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:填空题
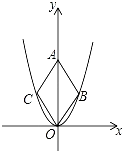 二次函数y=$\sqrt{6}$x2的图象如图,点O为坐标原点,点A在y轴的正半轴上,点B、C在二次函数y=$\sqrt{6}$x2的图象上,四边形OBAC为菱形,且∠OBA=120°,则菱形OBAC的面积为$\sqrt{3}$.
二次函数y=$\sqrt{6}$x2的图象如图,点O为坐标原点,点A在y轴的正半轴上,点B、C在二次函数y=$\sqrt{6}$x2的图象上,四边形OBAC为菱形,且∠OBA=120°,则菱形OBAC的面积为$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 销售单价x(元) | … | 230 | 235 | 240 | 245 | … |
| 销售量y(件) | … | 440 | 430 | 420 | 410 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一个长方形的纸片,长为a+6,宽为a-1,如图,在长方形纸片的四角剪裁处4个边长为1的正方形,沿着图中虚线折叠成一个无盖长方体纸盒,求纸盒的体积.
一个长方形的纸片,长为a+6,宽为a-1,如图,在长方形纸片的四角剪裁处4个边长为1的正方形,沿着图中虚线折叠成一个无盖长方体纸盒,求纸盒的体积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com