
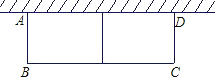
����Ŀ����ͼ��ʾ��ijũ���뽨��һ���ԣ�������ֲ���ֲ�ͬ�Ļ��ܣ��Թ�Ӧ�����г���Ҫ�����ó�Ϊ36m����ʣ�һ����ǽ��ǽ������ʹ�ó���l=13m����Χ���м����һ����ʵij����λ��ԣ��軨�Կ�ABΪx�����ΪS��
��1����S��x�ĺ�����ϵʽ����ָ������һ�κ��������Ƕ��κ�����
��2����ҪΧ�����Ϊ96m2�Ļ��ԣ����AB�ij��ȣ�
��3�����Ե�����ܴﵽ108m2�����ܣ������AB�ij��ȣ���������˵�����ɣ�
���𰸡���1��S=��36-3x��x=-3x2+36x��
��2��AB�ij�Ϊ8m��
��3�����Ե�������ܴﵽ108m2��
�������������������1��������ϵΪ������ʳ�-3AB����AB=S�����ɵó��𰸣�
��2��������ϵΪ������ʳ�-3AB����AB=96���������ֵ������ú��ʵĽ⼴�ɣ�
��3���ѣ�1�����ô���ʽ��ʾ���������Ϊa��x-h��2+b����ʽ�ɵ����������
�������������1���軨�Կ�ABΪx�����ΪS��
��S=��36-3x��x=-3x2+36x��
��2����AB�ij���x�ף�
��36-3x��x=96��
���x1=4��x2=8��
��x=4ʱ�������λ��Եij�Ϊ36-3x=24����ǽ�������ó���a��13m������ȥ��
��x=8ʱ�������λ��Եij�Ϊ24-3x=12���������⣻
��AB�ij�Ϊ8m��
��3�����Ե����ΪS=��36-3x��x=-3��x-6��2+108��
�൱AB��Ϊ6m����Ϊ16mʱ������������Ϊ108ƽ���ף�
�֡ߵ�AB=6mʱ�������λ��Եij�Ϊ36-3��6=18m����ǽ�������ó���a��13m������ȥ��
�ʻ��Ե�������ܴﵽ108m2��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���y=ax2+bx��ͼ����A��2��4����B��6��0����
��1����a��b��ֵ��
��2����C�Ǹö��κ���ͼ����A��B����֮���һ���㣬������Ϊx��2��x��6����д���ı���OACB�����S���ڵ�C�ĺ�����x�ĺ�������ʽ������S�����ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��:��ͼ����ƽ��ֱ������ϵ�У���ABC��������������ֱ�ΪA����2��1����B����1��4����C����3��2����
(1)������ABC����y��ԳƵ�ͼ����A1B1C1����ֱ��д��C1�����ꣻ
(2)��ԭ��OΪλ�����ģ�λ�Ʊ�Ϊ1��2����y�����࣬������ABC�Ŵ���ͼ����A2B2C2����ֱ��д��C2�����ꣻ
(3)�����D��a��b�����߶�AB�ϣ���ֱ��д��������2���ı仯��D�Ķ�Ӧ��D2��������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(2016�������п�)��ͼ����֪AC�ǡ�O��ֱ������B��Բ����(����A��C�غ�)����D��AC���ӳ����ϣ�����BD����O�ڵ�E������AOB��3��ADB����(����)

A. DE��EB B. ![]() DE��EB C.
DE��EB C. ![]() DE��DO D. DE��OB
DE��DO D. DE��OB
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪A�صĺ��θ߶�Ϊ��50�ף�B�ر�A�ظ�20�ף���B�صĺ��θ߶�Ϊ(����)
A. ��70��B. 20��C. ��30��D. 30��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2016����ļ���ȫ��������Ʒ���۶�6310��Ԫ����6310��Ԫ�ÿ�ѧ��������ʾӦΪԪ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������y=��k-1��x������ֵy���Ա���x��ֵ�������С����ôk��ȡֵ��Χ��_______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��ͬѧ��һ�����ʵ����У�ͨ����ij���߲���1�·���7�·ݵ��г��������ͳ�Ʒ�����ó����¹��ɣ�
�ٸ��߲˵����ۼ�![]() ����λ��Ԫ/ǧ�ˣ���ʱ��
����λ��Ԫ/ǧ�ˣ���ʱ��![]() ����λ���·ݣ������ϵ��
����λ���·ݣ������ϵ�� ![]() ��
��
�ڸ��߲˵�ƽ���ɱ�![]() ����λ��Ԫ/ǧ�ˣ���ʱ��
����λ��Ԫ/ǧ�ˣ���ʱ��![]() ����λ���·ݣ�������κ�����ϵ
����λ���·ݣ�������κ�����ϵ![]() ����֪4�·ݵ�ƽ���ɱ�Ϊ2Ԫ/ǧ�ˣ�6�·ݵ�ƽ���ɱ�Ϊ1Ԫ/ǧ�ˣ�
����֪4�·ݵ�ƽ���ɱ�Ϊ2Ԫ/ǧ�ˣ�6�·ݵ�ƽ���ɱ�Ϊ1Ԫ/ǧ�ˣ�
��1����ö��κ����Ľ���ʽ��
��2��������С��ͳ�ƵĽ��ۣ�������߲��ڵڼ��·ݵ�ƽ������![]() ����λ��Ԫ/ǧ�ˣ�������ƽ�������Ƕ��٣���ע��ƽ������
����λ��Ԫ/ǧ�ˣ�������ƽ�������Ƕ��٣���ע��ƽ������![]() ���ۼ�
���ۼ�![]() ƽ���ɱ���
ƽ���ɱ���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com