
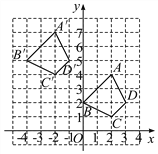
����Ŀ���ı���ABCD�����������ֱ�ΪA(2,4)��B(0,2)��C(2,1)��D(3,2)�����ı�������ƽ��4����λ���ȣ�������ƽ��3����λ���ȣ��õ��ı���A��B��C��D��.
(1)�ı���A��B��C��D�����ı���ABCD��Ӧ��ĺ�������ʲô��ϵ���������أ��ֱ�д��A��B��C��D�������ꣻ
(2)������ı���A��B��C��D�����������ı���ABCD����һ��ƽ�Ƶõ��ģ���ָ����һƽ�Ƶķ���;��룮
���𰸡�������.
���������������: (1)����ͼ��,�ֱ�д���ı���A��B��C��D�����ı���ABCD����������,�Աȷ���:��Ӧ��ĺ�����ֱ����4,������ֱ����3,A��(��2,7),B��(��4,5),C��(��2,4),D��(��1,5),
(2)����AA��,���ݹ��ɶ������:AA����![]() ��5.������ı���A��B��C��D�����������ı���ABCD����һ��ƽ�Ƶõ���,��ôƽ�Ƶķ�������A��A���ķ���,ƽ�Ƶľ�����5����λ����.
��5.������ı���A��B��C��D�����������ı���ABCD����һ��ƽ�Ƶõ���,��ôƽ�Ƶķ�������A��A���ķ���,ƽ�Ƶľ�����5����λ����.
�������:(1)�ı���A��B��C��D�����ı���ABCD���,��Ӧ��ĺ�����ֱ����4,������ֱ����3,A��(��2,7),B��(��4,5),C��(��2,4),D��(��1,5),
(2)����AA��,��AA����![]() ��5.���,������ı���A��B��C��D�����������ı���ABCD����һ��ƽ�Ƶõ���,��ôƽ�Ƶķ�������A��A���ķ���,ƽ�Ƶľ�����5����λ����.
��5.���,������ı���A��B��C��D�����������ı���ABCD����һ��ƽ�Ƶõ���,��ôƽ�Ƶķ�������A��A���ķ���,ƽ�Ƶľ�����5����λ����.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ȷ���ǣ�������
A. ���Ų�ͬ���������ǻ�Ϊ�෴��
B. һ�����������෴��һ���Ǹ�������
C. 2![]() ��2.75���ǩ�
��2.75���ǩ�![]() ���෴��
���෴��
D. 0û���෴��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����ר��������A��B�����ͺŵ�����Դ�����������۳�1��A�ͳ���3��B�ͳ������۶�Ϊ96��Ԫ���������۳�2��A�ͳ���1��B�ͳ������۶�Ϊ62��Ԫ��
��1����ÿ��A�ͳ���B�ͳ����ۼ۸�Ϊ����Ԫ��
��2����˾����õ깺��A��B�����ͺŵ�����Դ������6���������Ѳ�����130��Ԫ���Ҳ�����140��Ԫ�������ļ��ֹ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ABCD��PΪ����AB�ϵ�һ�㣬��BPΪ����������BPEF��ʹ��F���߶�CB���ӳ����ϣ�����EA��EC��
��1����ͼ1������P���߶�AB���ӳ����ϣ���֤��EA=EC��
��2������P���߶�AB�ϣ�
����ͼ2������AC����PΪAB���е�ʱ���жϡ�ACE����״����˵�����ɣ�
����ͼ3����AB=a��BP=b����EPƽ�֡�AECʱ����a��b����AEC�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣��ڳ�����ABCD�У�AB=DC=3cm��BC=5cm����P�ӵ�B��������1 cm/s���ٶ���BC���C�˶������P���˶�ʱ��Ϊts.
��1��PC= cm���ú�t�Ĵ���ʽ��ʾ��
��2����tΪ��ֵʱ����ABP�ա�DCP����˵������
��3����ͼ�ڣ�����P�ӵ�B��ʼ�˶�ʱ����Q�ӵ�C��������a cm/s���ٶ���CD���D�˶����Ƿ��������a��ֵ��ʹ����ABP����PCQȫ��?�����ڣ������a��ֵ���������ڣ���˵�����ɡ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��l1��ƽ��ֱ������ϵ�У�ֱ��l1��y�ύ�ڵ�A����B����3��3��Ҳ��ֱ��l1�ϣ�����B������ƽ��1����λ���ȣ�������ƽ��2����λ���ȵõ���C����Cǡ��Ҳ��ֱ��l1�ϣ�

��1�����C�������ֱ��l1�Ľ���ʽ��
��2��������C������ƽ��3����λ���ȣ�������ƽ��6����λ���ȵõ���D�������жϵ�D�Ƿ���ֱ��l1�ϣ�
��3����ֱ֪��l2��y=x+b������B����y�ύ�ڵ�E������ABE�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ں�����Сǿ����һ��������������Ҫ�����ɽ����һ�죬Сǿ��үү���ϣ�Ȼ����үү��ͼ�������߶ηֱ��ʾСǿ��үү�뿪ɽ�ŵľ��루�ף�����ɽ����ʱ�䣨�֣��Ĺ�ϵ����Сǿ��ʼ��ɽʱ��ʱ����

��1����1��(1)Сǿ��үү���϶����ף�
��2����2��(2)ɽ����ɽ�ŵľ����ж����ף�˭������ɽ����
��3����3��(3)Сǿ��������ʱ����үү?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������绥������ᣨ3rd World Internet Conference���������л������������ٰ�Ļ�����ʢ�ᣬ��2016��11��16����18�����㽭����ٰ죮ij����ѧУΪ���˽ⱾУѧ���Ա��λ��������Ĺ�ע�̶ȣ���ע�̶ȷ�Ϊ��A���ر��ע��B��һ���ע��C��ż����ע��D������ע���������ȡ�˲���ѧ�����е��飬����������Ƴ�Ƶ������ͳ��ͼ1������ͳ��ͼ2���������������ͼ����Ϣ�ش����⣮ 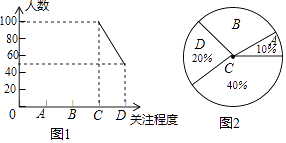
��1���˴γ��������У��������˶�����ѧ����
��2�����ͼ2������B���Ե�Բ�ĽǶ���������ͼ1����������
��3������ε����У��ţ�1����мס��ҡ����������ˡ��ر��ע�����컥������ᣬ�����������������ȡ���˽��н����������б�������״ͼ�ķ��������ȡ������ǡ���Ǽ��ҵĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ƽ��ֱ������ϵ����������M��x1�� y1����N��x2��y2������|x1��x2|+|y1��y2|ΪM��N����Ĺ��ɾ��룬������d��M��N�����磺M��2����3����N��1��4������d��M��N��=|2��1|+|��3��4|=8. ��P��x0��y0����һ���㣬Q��x��y����ֱ��y=kx+b�ϵ�һ���㣬��d��P��Q������СֵΪP��ֱ��y=kx+b�Ĺ��ɾ��룮��P��-3,2����ֱ��![]() �Ĺ��ɾ���Ϊ�� ��
�Ĺ��ɾ���Ϊ�� ��
A. ![]() B.
B. ![]() C. 3 D. 4
C. 3 D. 4
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com