Question

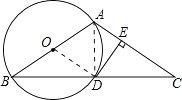
【题目】已知：如图，在△ABC中，AB=AC，以AB为直径的⊙O交BC于点D，过点D作DE⊥AC于点E．
（1）请说明DE是⊙O的切线；
（2）若∠B=30°，AB=8，求DE的长．

Answer 1

【答案】
（1）解：连接OD，则OD=OB，

∴∠B=∠ODB．

∵AB=AC，

∴∠B=∠C．

∴∠ODB=∠C．

∴OD∥AC．（2分）

∴∠ODE=∠DEC=90°．

∴DE是⊙O的切线．

（2）解：连接AD，

∵AB是⊙O的直径，

∴∠ADB=90°．（1分）

∴ ．（2分）

又∵AB=AC，

∴CD=BD= ，∠C=∠B=30°．（2分）

∴ ．（1分）

【解析】（1）要想证DE是⊙O的切线，只要连接OD，求证∠ODE=90°即可．（2）利用直角三角形和等边三角形的特点来求DE的长．
【考点精析】本题主要考查了切线的判定定理和解直角三角形的相关知识点，需要掌握切线的判定方法：经过半径外端并且垂直于这条半径的直线是圆的切线；解直角三角形的依据：①边的关系a2+b2=c2；②角的关系：A+B=90°；③边角关系：三角函数的定义．(注意：尽量避免使用中间数据和除法)才能正确解答此题．