
【题目】( 本小题满分10分)如图,已知:在平行四边形ABCD中,点E、F、G、H分别在边AB、BC、CD、DA上,AE=CG,AH=CF,且EG平分∠HEF.求证:
⑴△AEH≌△CGF;
⑵四边形EFGH是菱形.

【答案】(1)证明见试题解析;(2)证明见试题解析.
【解析】试题分析:(1)、由全等三角形的判定定理SAS证得结论;(2)、易证四边形EFGH是平行四边形,那么EF∥GH,那么∠HGE=∠FEG,而EG是角平分线,易得∠HEG=∠FEG,根据等量代换可得∠HEG=∠HGE,从而有HE=HG,易证四边形EFGH是菱形.
试题解析:(1)、如图,∵四边形ABCD是平行四边形, ∴∠A=∠C,
在△AEH与△CGF中,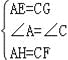 , ∴△AEH≌△CGF(SAS);
, ∴△AEH≌△CGF(SAS);
(2)、∵四边形ABCD是平行四边形, ∴AB=CD,AD=BC,∠B=∠D. 又∵AE=CG,AH=CF,
∴BE=DG,BF=DH, 在△BEF与△DGH中,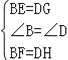 ∴△BEF≌△DGH(SAS), ∴EF=GH.
∴△BEF≌△DGH(SAS), ∴EF=GH.
又由(1)知,△AEH≌△CGF, ∴EH=GF, ∴四边形EFGH是平行四边形, ∴HG∥EF,
∴∠HGE=∠FEG, ∵EG平分∠HEF, ∴∠HEG=∠FEG, ∴∠HEG=∠HGE, ∴HE=HG,∴四边形EFGH是菱形.


科目:初中数学 来源: 题型:
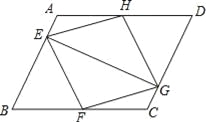
【题目】如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作EF∥AD,与AC、DC分别交于点G、F,H为CG的中点,连接DE、EH、DH、FH.下列结论:①EG=DF;②∠AEH+∠ADH=180°;③△EHF≌△DHC;④若 ![]() =
= ![]() ,则3S△EDH=13S△DHC , 其中结论正确的有(填写序号).
,则3S△EDH=13S△DHC , 其中结论正确的有(填写序号). 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为进一步落实《中华人民共和国民办教育促进法》,某市教育局拿出了b元资金建立民办教育发展基金会,其中一部分作为奖金发给了n所民办学校.奖金分配方案如下:首先将n所民办学校按去年完成教育、教学工作业绩(假设工作业绩均不相同)从高到低,由1到n排序,第1所民办学校得奖金![]() 元,然后再将余额除以n发给第2所民办学校,按此方法将奖金逐一发给了n所民办学校.
元,然后再将余额除以n发给第2所民办学校,按此方法将奖金逐一发给了n所民办学校.
(1)请用n、b分别表示第2所、第3所民办学校得到的奖金;
(2)设第k所民办学校所得到的奖金为![]() 元(1
元(1 ![]() ),试用k、n和b表示
),试用k、n和b表示![]() (不必证明);
(不必证明);
(3)比较![]() 和
和![]() 的大小(k=1,2 ,……,
的大小(k=1,2 ,……, ![]() ),并解释此结果关于奖金分配原则的实际意义.
),并解释此结果关于奖金分配原则的实际意义.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明解方程![]() -
-![]() =1的过程如下:
=1的过程如下:
解:方程两边乘x,得1-(x-2)=1.①
去括号,得1-x-2=1.②
移项,得-x=1-1+2.③
合并同类项,得-x=2.④
解得x=-2.⑤
所以,原分式方程的解为x=-2.⑥
请指出他解答过程中的错误,并写出正确的解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC于点E. 
(1)请说明DE是⊙O的切线;
(2)若∠B=30°,AB=8,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用一个直径为10cm的玻璃球和一个圆锥形的牛皮纸纸帽制作一个不倒翁玩具,不倒翁的轴截面如图所示,圆锥的母线AB与⊙O相切于点B,不倒翁的顶点A到桌面L的最大距离是18cm.若将圆锥形纸帽表面全涂上颜色,则涂色部分的面积为cm2 . 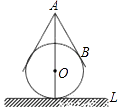
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com