
【题目】如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作EF∥AD,与AC、DC分别交于点G、F,H为CG的中点,连接DE、EH、DH、FH.下列结论:①EG=DF;②∠AEH+∠ADH=180°;③△EHF≌△DHC;④若 ![]() =
= ![]() ,则3S△EDH=13S△DHC , 其中结论正确的有(填写序号).
,则3S△EDH=13S△DHC , 其中结论正确的有(填写序号). 
【答案】①②③
【解析】解:①∵四边形ABCD为正方形,EF∥AD, ∴EF=AD=CD,∠ACD=45°,∠GFC=90°,
∴△CFG为等腰直角三角形,
∴GF=FC,
∵EG=EF﹣GF,DF=CD﹣FC,
∴EG=DF,故①正确;
②∵△CFG为等腰直角三角形,H为CG的中点,
∴FH=CH,∠GFH= ![]() ∠GFC=45°=∠HCD,
∠GFC=45°=∠HCD,
在△EHF和△DHC中, 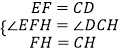 ,
,
∴△EHF≌△DHC(SAS),
∴∠HEF=∠HDC,
∴∠AEH+∠ADH=∠AEF+∠HEF+∠ADF﹣∠HDC=∠AEF+∠ADF=180°,故②正确;
③∵△CFG为等腰直角三角形,H为CG的中点,
∴FH=CH,∠GFH= ![]() ∠GFC=45°=∠HCD,
∠GFC=45°=∠HCD,
在△EHF和△DHC中, 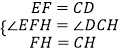 ,
,
∴△EHF≌△DHC(SAS),故③正确;
④∵ ![]() =
= ![]() ,
,
∴AE= ![]() BE,
BE,
∵△CFG为等腰直角三角形,H为CG的中点,
∴FH=GH,∠FHG=90°,
∵∠EGH=∠FHG+∠HFG=90°+∠HFG=∠HFD,
在△EGH和△DFH中, 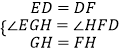 ,
,
∴△EGH≌△DFH(SAS),
∴∠EHG=∠DHF,EH=DH,∠DHE=∠EHG+∠DHG=∠DHF+∠DHG=∠FHG=90°,
∴△EHD为等腰直角三角形,
过H点作HM垂直于CD于M点,如图所示: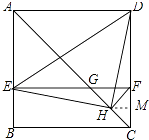
设HM=x,则DM=2x,DH= ![]() x,CD=3x,
x,CD=3x,
则S△DHC= ![]() ×HM×CD=
×HM×CD= ![]() x2 , S△EDH=
x2 , S△EDH= ![]() ×DH2=
×DH2= ![]() x2 ,
x2 ,
∴3S△EDH=5S△DHC , 故④错误;
故答案为:①②③.
①根据题意可知∠ACD=45°,则GF=FC,则EG=EF﹣GF=CD﹣FC=DF;
②由SAS证明△EHF≌△DHC,得到∠HEF=∠HDC,从而∠AEH+∠ADH=∠AEF+∠HEF+∠ADF﹣∠HDC=180°;
③同②证明△EHF≌△DHC即可;
④若 ![]() =
= ![]() ,则AE=
,则AE= ![]() BE,可以证明△EGH≌△DFH,则∠EHG=∠DHF且EH=DH,则∠DHE=90°,△EHD为等腰直角三角形,过H点作HM垂直于CD于M点,设HM=x,则DM=2x,DH=
BE,可以证明△EGH≌△DFH,则∠EHG=∠DHF且EH=DH,则∠DHE=90°,△EHD为等腰直角三角形,过H点作HM垂直于CD于M点,设HM=x,则DM=2x,DH= ![]() x,CD=6x,则S△DHC=
x,CD=6x,则S△DHC= ![]() ×HM×CD=
×HM×CD= ![]() x2 , S△EDH=
x2 , S△EDH= ![]() ×DH2=
×DH2= ![]() x2 .
x2 .


科目:初中数学 来源: 题型:
【题目】已知一个长方形绿化带的长为(6a+4b)米,宽为(3a﹣2b)米.
(1)求该绿化带的面积(用含有a、b的代数式表示);
(2)当a=10,b=5时,该绿化带的面积是多少平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在长方形ABCD中,AB=DC=3cm,BC=5cm,点P从点B出发,以1 cm/s的速度沿BC向点C运动,设点P的运动时间为ts.
(1)PC= cm(用含t的代数式表示)
(2)当t为何值时,△ABP≌△DCP,请说明理由
(3)如图②,当点P从点B开始运动时,点Q从点C出发,以a cm/s的速度沿CD向点D运动,是否存在这样a的值,使得△ABP与△PCQ全等?若存在,请求出a的值,若不存在,请说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王教授和孙子小强经常一起进行早锻炼,主要活动是爬山.有一天,小强让爷爷先上,然后追赶爷爷.图中两条线段分别表示小强和爷爷离开山脚的距离(米)与爬山所用时间(分)的关系(从小强开始爬山时计时).

【1】【1】(1)小强让爷爷先上多少米?
【2】【2】(2)山顶离山脚的距离有多少米?谁先爬上山顶?
【3】【3】(3)小强经过多少时间追上爷爷?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第三届世界互联网大会(3rd World Internet Conference),是由中华人民共和国倡导并举办的互联网盛会,于2016年11月16日至18日在浙江乌镇举办.某初中学校为了了解本校学生对本次互联网大会的关注程度(关注程度分为:A.特别关注;B.一般关注;C.偶尔关注;D.不关注),随机抽取了部分学生进行调查,并将结果绘制成频数折线统计图1和扇形统计图2(不完整)请根据图中信息回答问题. 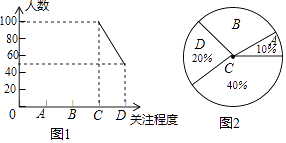
(1)此次抽样调查中,共调查了多少名学生?
(2)求出图2中扇形B所对的圆心角度数,并将图1补充完整.
(3)在这次调查中,九(1)班共有甲、乙、丙、丁四人“特别关注”本届互联网大会,现准备从四人中随机抽取两人进行交流,请用列表法或画树状图的方法求出抽取的两人恰好是甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两位采购员同去一家饲料公司购买两次饲料.两次饲料的价格有变化,两位采购员的购货方式也不同,其中,甲每次购买1000千克,乙每次用去800元,而不管购买多少饲料.
(1)甲、乙所购饲料的平均单价各是多少?
(2)谁的购货方式更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】( 本小题满分10分)如图,已知:在平行四边形ABCD中,点E、F、G、H分别在边AB、BC、CD、DA上,AE=CG,AH=CF,且EG平分∠HEF.求证:
⑴△AEH≌△CGF;
⑵四边形EFGH是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场经营A种品牌的玩具,购进时间的单价是30元,但据市场调查,在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.
(1)不妨设该种品牌玩具的销售单价为x元(x>40),请用含x的代数式表示该玩具的销售量;
(2)若玩具厂规定该品牌玩具销售单价不低于44元,且商场要完成不少于450件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?
(3)该商场计划将(2)中所得的利润的一部分资金采购一批B种玩具并转手出售,根据市场调查并准备两种方案,方案①:如果月初出售,可获利15%,并可用本和利再投资C种玩具,到月末又可获利10%;方案②:如果只到月末出售可直接获利30%,但要另支付他库保管费350元,请问商场如何使用这笔资金,采用哪种方案获利较多?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com