
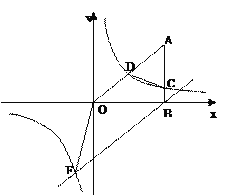
【题目】(本题8分)如图, ![]() 轴于点
轴于点![]() ,
,  ,反比例函数
,反比例函数![]() 与OA、AB分别相交于点D、C,且点D为OA的中点.
与OA、AB分别相交于点D、C,且点D为OA的中点.
(1)求反比例函数的解析式;
(2)过点B的直线![]() 与反比例函数
与反比例函数![]() 图象交于第三象限内一点F,求四边形
图象交于第三象限内一点F,求四边形![]() 的面积.
的面积.
【答案】![]()
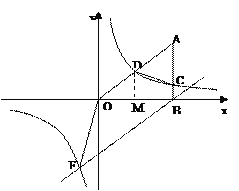
解:过D作DM⊥x轴交OB于点M。
∵AB⊥x轴于B, ∴∠DMO=∠ABO=90°∴DM∥AB,
∴![]() ,而D为OA中点,
,而D为OA中点, ![]()
DM=![]() ,又∵
,又∵![]() ,
,![]()
∴OB=8,AB=6,∴OM=4,DM=3
∴![]() =3×4=12
=3×4=12
∴反比例函数的解析式为: ![]()
(2)将![]() 代入
代入![]() 得
得![]() ,联立
,联立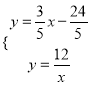
得![]() ,∴F(-2,-6),∴
,∴F(-2,-6),∴![]() =
=![]() =
=![]() =48.
=48.

【解析】试题解析:试题分析:(1)过点D作DM⊥x轴,通过正弦函数得出AB的长,即可得出A的坐标,进而得出D的坐标,代入 ![]() ,根据待定系数法即可求得;
,根据待定系数法即可求得;
(2)易求得直线BF的解析式,然后联立方程求得F的坐标,过点F作FN⊥x轴,
根据S四边形OFBA=S△AOB+S△BOF求得即可.
解:过D作DM⊥x轴交OB于点M。
∵AB⊥x轴于B, ∴∠DMO=∠ABO=90°∴DM∥AB,
∴![]() ,而D为OA中点,
,而D为OA中点, ![]()
DM=![]() ,又∵
,又∵![]() ,
,![]()
∴OB=8,AB=6,∴OM=4,DM=3
∴![]() =3×4=12
=3×4=12
∴反比例函数的解析式为: ![]()
(2)将![]() 代入
代入![]() 得
得![]() ,联立
,联立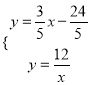
得![]() ,∴F(-2,-6),∴
,∴F(-2,-6),∴![]() =
=![]() =
=![]() =48.
=48.


科目:初中数学 来源: 题型:
【题目】(本小题满分12分)在△ABC中,AB=AC,P是BC上任意一点.
(1)如图①,若P是BC边上任意一点,PF⊥AB于点F,PE⊥AC于点E,BD为△ABC的高线,试探求PE,PF与BD之间的数量关系;

(2)如图②,若P是BC延长线上一点,PF⊥AB于点F,PE⊥AC于点E,CD为△ABC的高线,试探求PE,PF与CD之间的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O为原点,点A(4,0),点B(0,3),把△ABO绕点B逆时针旋转,得△A′BO′,点A,O旋转后的对应点为A′,O′,记旋转角为α.
(1)如图①,若α=90°,求AA′的长;
(2)如图②,若α=120°,求点O′的坐标;
(3)在(2)的条件下,边OA上 的一点P旋转后的对应点为P′,当O′P+BP′取得最小值时,求点P′的坐标(直接写出结果即可)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个工程队共同承担一项筑路任务,甲队单独施工完成此项任务比乙队单独施工完成此项任务多用10天,且甲队单独施工45天和乙队单独施工30天的工作量相同.
(1)甲、乙两队单独完成此项任务各需多少天?
(2)若甲、乙两队共同工作了3天后,乙队因设备检修停止施工,由甲队继续施工,为了不影响工程进度,甲队的工作效率提高到原来的2倍,要使甲队总的工作量不少于乙队的工作量的2倍,那么甲队至少再单独施工多少天?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com