
【题目】如图所示的一块地,∠ADC=90°,AD=12m,CD=9m,AB=39m,BC=36m,求这块地的面积.

【答案】216平方米.
【解析】试题分析:连接AC,根据直角△ACD可以求得斜边AC的长度,根据AC,BC,AB可以判定△ABC为直角三角形,要求这块地的面积,求△ABC与△ACD的面积之差即可.
解:连接AC,
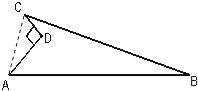
已知,在直角△ACD中,CD=9m,AD=12m,
根据AD2+CD2=AC2,可以求得AC=15m,
在△ABC中,AB=39m,BC=36m,AC=15m,
∴存在AC2+CB2=AB2,
∴△ABC为直角三角形,
要求这块地的面积,求△ABC和△ACD的面积之差即可,
S=S△ABC﹣S△ACD=![]() ACBC﹣
ACBC﹣![]() CDAD,
CDAD,
=![]() ×15×36﹣
×15×36﹣![]() ×9×12,
×9×12,
=270﹣54,
=216m2,
答:这块地的面积为216m2.


科目:初中数学 来源: 题型:
【题目】(满分8分)在北海市创建全国文明城活动中,需要20名志愿者担任“讲文明树新风”公益广告宣传工作,其中男生8人,女生12人.
(1)若从这20人中随机选取一人作为“展板挂图”讲解员,求选到女生的概率;
(2)若“广告策划”只在甲、乙两人中选一人,他们准备以游戏的方式决定由谁担任,游戏规则如下:将四张牌面数字分别为2,3,4,5的扑克牌洗匀后,数字朝下放于桌面,从中任取2张,若牌面数字之和为偶数,则甲担任,否则乙担任.试问这个游戏公平吗?请用树状图或列表法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正三角形A1B1C1的面积为1,取ΔA1B1C1各边的中点A2、B2、C2,作第二个正三角形A2B2C2,再取ΔA2B2C2各边的中点A3、B3、C3,作第三个正三角形A3B3C3,……,则第4个正三角形A4B4C4的面积是__________;第n个正三角形AnBnCn的面积是_____________。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰△BDC的顶点在等边三角形ABC的内部,∠BDC=90°,连接AD,过点D作一条直线将△ABD分割成两个等腰三角形,则分割出来的这两个等腰三角形的顶角度数分别是_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个三角形是轴对称图形,且有一个内角是60°,那么这个三角形是( )
A.等边三角形
B.等腰直角三角形
C.等腰三角形
D.含30°角的直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
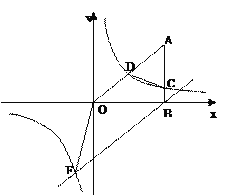
【题目】(本题8分)如图, ![]() 轴于点
轴于点![]() ,
,  ,反比例函数
,反比例函数![]() 与OA、AB分别相交于点D、C,且点D为OA的中点.
与OA、AB分别相交于点D、C,且点D为OA的中点.
(1)求反比例函数的解析式;
(2)过点B的直线![]() 与反比例函数
与反比例函数![]() 图象交于第三象限内一点F,求四边形
图象交于第三象限内一点F,求四边形![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com