
【题目】已知三角形的第一条边的长是![]() ,第二条边长是第一条边长的2倍少3,第三条边比第二条边短5。
,第二条边长是第一条边长的2倍少3,第三条边比第二条边短5。
(1)用含![]() 、
、![]() 的式子表示这个三角形的周长;
的式子表示这个三角形的周长;
(2)当![]() ,
,![]() 时,求这个三角形的周长;
时,求这个三角形的周长;
(3)当![]() ,三角形的周长为 39时,求各边长。
,三角形的周长为 39时,求各边长。
科目:初中数学 来源: 题型:
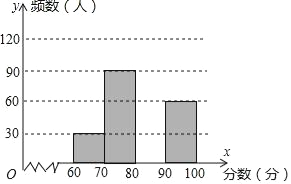
【题目】为了了解我市中学生参加“科普知识”竞赛成绩的情况,随机抽查了部分参赛学生的成绩,整理并制作出如下的统计表和统计图,如图所示.请根据图表信息解答下列问题:
组别 | 分数段(分) | 频数 | 频率 |
A组 | 60≤x<70 | 30 | 0.1 |
B组 | 70≤x<80 | 90 | n |
C组 | 80≤x<90 | m | 0.4 |
D组 | 90≤x<100 | 60 | 0.2 |
(1)在表中:m= ,n= ;
(2)补全频数分布直方图;
(3)4个小组每组推荐1人,然后从4人中随机抽取2人参加颁奖典礼,恰好抽中A、C两组学生的概率是多少?并列表或画树状图说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、D、C、F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加一个条件是( )

A. ∠BCA=∠F; B. ∠B=∠E; C. BC∥EF ; D. ∠A=∠EDF
查看答案和解析>>
科目:初中数学 来源: 题型:
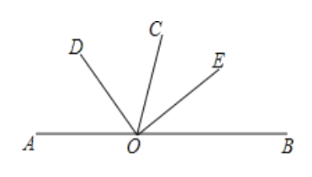
【题目】如图,点O是直线AB上一点,OC为任一条射线,OD平分∠AOC,OE平分∠BOC.
(1)分别写出图中∠AOD和∠AOC的补角
(2)求∠DOE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y=![]() (k>0)的图象与一次函数y=
(k>0)的图象与一次函数y=![]() x的图象交于A、B两点(点A在第一象限).
x的图象交于A、B两点(点A在第一象限).

(1)当点A的横坐标为4时.
①求k的值;
②根据反比例函数的图象,直接写出当﹣4<x<2(x≠0)时,y的取值范围;
(2)点C为y轴正半轴上一点,∠ACB=90°,且△ACB的面积为10,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
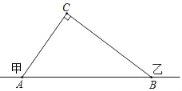
【题目】在甲村至乙村间有一条公路,在C处需要爆破,已知点C与公路上的停靠站A的距离为300米,与公路上的另一停靠站B的距离为400米,且CA⊥CB,如图所示,为了安全起见,爆破点C周围半径250米范围内不得进入,问:在进行爆破时,公路AB段是否有危险?是否需要暂时封锁?请用你学过的知识加以解答.
查看答案和解析>>
科目:初中数学 来源: 题型:
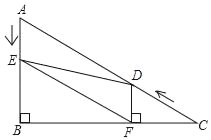
【题目】如图,在Rt△ABC中,∠B=90°,AC=12,∠A=60°.点D从点C出发沿CA方向以每秒2个单位长的速度向A点匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
(1)AB的长是 .
(2)在D、E的运动过程中,线段EF与AD的关系是否发生变化?若不变化,那么线段EF与AD是何关系,并给予证明;若变化,请说明理由.
(3)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,以AC为直径作⊙O,交AB于D,过点O作OE∥AB,交BC于E.
(1)求证:ED为⊙O的切线;
(2)如果⊙O的半径为![]() ,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.
,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.

【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)首先连接OD,由OE∥AB,根据平行线与等腰三角形的性质,易证得![]() ≌
≌![]() 即可得
即可得![]() ,则可证得
,则可证得![]() 为
为![]() 的切线;
的切线;
(2)连接CD,根据直径所对的圆周角是直角,即可得![]() 利用勾股定理即可求得
利用勾股定理即可求得![]() 的长,又由OE∥AB,证得
的长,又由OE∥AB,证得![]() 根据相似三角形的对应边成比例,即可求得
根据相似三角形的对应边成比例,即可求得![]() 的长,然后利用三角函数的知识,求得
的长,然后利用三角函数的知识,求得![]() 与
与![]() 的长,然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案.
的长,然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案.
试题解析:(1)证明:连接OD,

∵OE∥AB,
∴∠COE=∠CAD,∠EOD=∠ODA,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠COE=∠DOE,
在△COE和△DOE中,
 ∴△COE≌△DOE(SAS),
∴△COE≌△DOE(SAS),
![]()
∴ED⊥OD,
∴ED是![]() 的切线;
的切线;
(2)连接CD,交OE于M,
在Rt△ODE中,
∵OD=32,DE=2,
![]()
∵OE∥AB,
∴△COE∽△CAB,
![]() ∴AB=5,
∴AB=5,
∵AC是直径,
![]()
![]()
![]()
![]()
∵EF∥AB,
![]()
![]()
![]()
∴S△ADF=S梯形ABEFS梯形DBEF
![]()
∴△ADF的面积为![]()

【题型】解答题
【结束】
25
【题目】【题目】已知,抛物线y=ax2+ax+b(a≠0)与直线y=2x+m有一个公共点M(1,0),且a<b.
(1)求b与a的关系式和抛物线的顶点D坐标(用a的代数式表示);
(2)直线与抛物线的另外一个交点记为N,求△DMN的面积与a的关系式;
(3)a=﹣1时,直线y=﹣2x与抛物线在第二象限交于点G,点G、H关于原点对称,现将线段GH沿y轴向上平移t个单位(t>0),若线段GH与抛物线有两个不同的公共点,试求t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为鼓励学生参加体育锻炼,学校计划拿出不超过3200元的资金购买一批篮球和
排球,已知篮球和排球的单价比为3:2,单价和为160元.
(1)篮球和排球的单价分别是多少元?
(2)若要求购买的篮球和排球的总数量是36个,且购买的排球数少于11个,有哪几种购买方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com