Question

【题目】如图，点D是等边△ABC中BC边的延长线上一点，且AC=CD，以AB为直径作⊙O，分别交边AC、BC于点E、点F

（1）求证：AD是⊙O的切线；
（2）连接OC，交⊙O于点G，若AB=4，求线段CE、CG与围成的阴影部分的面积S．

Answer 1

【答案】
（1）

证明：∵△ABC为等边三角形，

∴AC=BC，

又∵AC=CD，

∴AC=BC=CD，

∴△ABD为直角三角形，

∴AB⊥AD，

∵AB为直径，

∴AD是⊙O的切线；

（2）

解：连接OE，

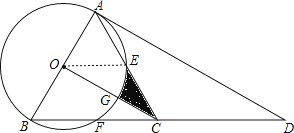
∵OA=OE，∠BAC=60°，

∴△OAE是等边三角形，

∴∠AOE=60°，

∵CB=BA，OA=OB，

∴CO⊥AB，

∴∠AOC=90°，

∴∠EOC=30°，

∵△ABC是边长为4的等边三角形，

∴AO=2，由勾股定理得：OC==2，

同理等边三角形AOE边AO上高是=，

S阴影=S△AOC﹣S等边△AOE﹣S扇形EOG==．

【解析】（1）求出∠DAC=30°，即可求出∠DAB=90°，根据切线的判定推出即可；
（2）连接OE，分别求出△AOE、△AOC，扇形OEG的面积，即可求出答案．
【考点精析】解答此题的关键在于理解切线的判定定理的相关知识，掌握切线的判定方法：经过半径外端并且垂直于这条半径的直线是圆的切线，以及对扇形面积计算公式的理解，了解在圆上，由两条半径和一段弧围成的图形叫做扇形；扇形面积S=π（R2-r2）．