
【题目】已知:AB、CD为⊙O的直径,弦BE交CD于点F,连接DE交AB于点G,GO=GD.
(1)如图1,求证:DE=DF; 
(2)如图2,作弦AK∥DC,AK交BE于点N,连接CK,求证:四边形KNFC为平行四边形; 
(3)如图3,作弦CH,连接DH,∠CDH=3∠EDH,CH=2 ![]() ,BE=4
,BE=4 ![]() ,求DH的长.
,求DH的长. 
【答案】
(1)证明:如图1中,连接BC.
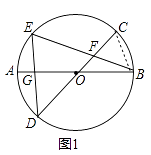
∵OB=OC,
∴∠C=∠OBC=∠E,
∵GO=GD,
∴∠D=∠GOD=∠EBC=∠BOC,
∵∠OBC=∠EBC+∠EBA,∠EFD=∠BOC+∠EBA,
∵∠EBC=∠BOC,
∴∠OBC=∠EFD=∠E,
∴DE=DF.
(2)证明:如图2中,连接AD、DK、BC.
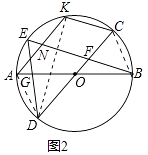
∵AK∥CD,
∴∠AKD=∠KDC,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴∠ADC=∠KCD,
∵∠ADO=∠OBC=∠OCB=∠E=∠EFD,
∴∠KCD=∠EFD,
∴KC∥FN,∵KN∥FC,
∴四边形KNFC是平行四边形.
(3)解:如图3中,作ON⊥BE于N,HK⊥CD于K,连接EO.
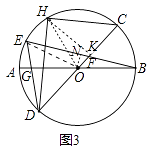
∵ON⊥EB,
∴EN=BN=2 ![]() ,
,
∵∠CDH=3∠EDH,
设∠EDH=x,则∠CDH=3x,∠OHD=∠ODH=3x,∠HOC=∠D+∠OHD=6x,∠GOD=∠GDO=∠BOC=4x,∠HOB=∠HOC+∠BOC=10x,∠EOC=∠ODE+∠OED=8x,∠EOB=∠EOC+∠BOC=12x,
∵∠BON=∠EON=6x,
∴∠HOK=∠BON=6x,
在△OHK和△OBN中,
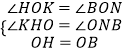 ,
,
∴△OHK≌△OBN,
∴HK=BN=2 ![]() ,
,
在Rt△CHK中,CK= ![]() =
= ![]() =4,
=4,
∵CD是直径,
∴∠CHD=∠CKH=90°,
∵∠C=∠C,
∴△CKH∽△CHD,
∴ ![]() =
= ![]() ,
,
∴DH= ![]() =
= ![]() =
= ![]() .
.
【解析】(1)如图1中,连接BC.欲证明DE=DF,只要证明∠E=∠EFD.(2)如图2中,连接AD、DK、BC.首先证明∠ADC=∠KCD,再证明∠EFD=∠ADC,即可推出∠EFD=∠KCD,推出KC∥FN,由此即可解决问题.(3)如图3中,作ON⊥BE于N,HK⊥CD于K,连接EO.想办法证明△OHK≌△OBN,推出HK=BN=2 ![]() ,再证明△CKH∽△CHD,得
,再证明△CKH∽△CHD,得 ![]() =
= ![]() ,利用勾股定理求出KC即可解决问题.
,利用勾股定理求出KC即可解决问题.


科目:初中数学 来源: 题型:
【题目】设点Q到图形W上每一个点的距离的最小值称为点Q到图形W的距离.例如正方形ABCD满足A(1,0),B(2,0),C(2,1),D(1,1),那么点O(0,0)到正方形ABCD的距离为1. 
(1)如果⊙P是以(3,4)为圆心,1为半径的圆,那么点O(0,0)到⊙P的距离为;
(2)求点M(3,0)到直线y=2x+1的距离;
(3)如果点N(0,a)到直线y=2x+1的距离为3,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某工艺品厂生产一款工艺品、已知这款工艺品的生产成本为每件60元. 经市场调研发现:该款工艺品每天的销售量y(件)与售价x(元)之间存在着如下表所示的一次函数关系.
售价x(元) | … | 70 | 90 | … |
销售量y(件) | … | 3000 | 1000 | … |
(利润=(售价﹣成本价)×销售量)
(1)求销售量y(件)与售价x(元)之间的函数关系式;
(2)你认为如何定价才能使工艺品厂每天获得的利润为40000元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=ax+1与x轴、y轴分别相交于A、B两点,与双曲线y= ![]() (x>0)相交于点P,PC⊥x轴于点C,且PC=2,点A的坐标为(﹣2,0).
(x>0)相交于点P,PC⊥x轴于点C,且PC=2,点A的坐标为(﹣2,0).
(1)求双曲线的解析式;
(2)若点Q为双曲线上点P右侧的一点,且QH⊥x轴于H,当以点Q、C、H为顶点的三角形与△AOB相似时,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在研究相似问题时,甲、乙同学的观点如下: 甲:将边长为3、4、5的三角形按图1的方式向外扩张,得到新三角形,它们的对应边间距为1,则新三角形与原三角形相似.
乙:将邻边为3和5的矩形按图2的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形不相似.
对于两人的观点,下列说法正确的是( )
A.两人都对
B.两人都不对
C.甲对,乙不对
D.甲不对,乙对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为全面开展“阳光大课间”活动,某中学三个年级准备成立“足球”、“篮球”、“跳绳”、“踢毽”四个课外活动小组,学校体育组根据七年级学生的报名情况(每人限报一项)绘制了两幅不完整的统计图(如图), 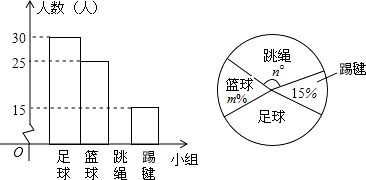
请根据以上信息,完成下列问题:
(1)m= , n= , 并将条形统计图补充完整;
(2)根据七年级的报名情况,试问全校2000人中,大约有多少人报名参加足球活动小组?
(3)根据活动需要,从“跳绳”小组的二男二女四名同学中随机选取两人到“踢毽”小组参加训练,请用列表或树状图的方法计算恰好选中一男一女两名同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D是等边△ABC中BC边的延长线上一点,且AC=CD,以AB为直径作⊙O,分别交边AC、BC于点E、点F
(1)求证:AD是⊙O的切线;
(2)连接OC,交⊙O于点G,若AB=4,求线段CE、CG与![]() 围成的阴影部分的面积S.
围成的阴影部分的面积S.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com