
【题目】计算下列各式
(1)2cos45°+sin30°cos60°+cos30°
(2)| ![]() ﹣5|+2cos30°+(
﹣5|+2cos30°+( ![]() )﹣1+(9﹣
)﹣1+(9﹣ ![]() )0+
)0+ ![]() .
.
【答案】
(1)解:2cos45°+sin30°cos60°+cos30°
=2× ![]() +
+ ![]() ×
× ![]() +
+ ![]()
= ![]() +
+ ![]() +
+ ![]() ;
;
(2)解:| ![]() ﹣5|+2cos30°+(
﹣5|+2cos30°+( ![]() )﹣1+(9﹣
)﹣1+(9﹣ ![]() )0+
)0+ ![]()
=5﹣ ![]() +2×
+2× ![]() +3+1+2
+3+1+2
=5﹣ ![]() +
+ ![]() +3+1+2
+3+1+2
=11.
【解析】(1)本题涉及特殊角的三角函数值的考点.在计算时,根据实数的运算法则求得计算结果.(2)本题涉及绝对值、特殊角的三角函数值、负整数指数幂、零指数幂、二次根式化简5个考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.
【考点精析】本题主要考查了零指数幂法则和整数指数幂的运算性质的相关知识点,需要掌握零次幂和负整数指数幂的意义: a0=1(a≠0);a-p=1/ap(a≠0,p为正整数);aman=am+n(m、n是正整数);(am)n=amn(m、n是正整数);(ab)n=anbn(n是正整数);am/an=am-n(a不等于0,m、n为正整数);(a/b)n=an/bn(n为正整数)才能正确解答此题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)图象过点(﹣1,0),顶点为(1,2),则结论:
①abc>0;②x=1时,函数最大值是2;③4a+2b+c>0;④2a+b=0;⑤2c<3b.
其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为参加学校的“我爱古诗词”知识竞赛,小王所在班级组织了一次古诗词知识测试,并将全班同学的分数(得分取正整数,满分为100分)进行统计,以下是根据这次测试成绩制作的不完整的频率分布表和频率分布直方图.
组别 | 分组 | 频数 | 频率 |
1 | 50≤x<60 | 9 | 0.18 |
2 | 60≤x<70 | a | |
3 | 70≤x<80 | 20 | 0.40 |
4 | 80≤x<90 | 0.08 | |
5 | 90≤x≤100 | 2 | b |
合计 |

请根据以上频率分布表和频率分布直方图,回答下列问题:
(1)求出a、b、x、y的值;
(2)若要从小明、小敏等五位成绩优秀的同学中随机选取两位参加竞赛,请用“列表法”或“树状图”求出小明、小敏同时被选中的概率.(注:五位同学请用A、B、C、D、E表示,其中小明为A,小敏为B)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:AB、CD为⊙O的直径,弦BE交CD于点F,连接DE交AB于点G,GO=GD.
(1)如图1,求证:DE=DF; 
(2)如图2,作弦AK∥DC,AK交BE于点N,连接CK,求证:四边形KNFC为平行四边形; 
(3)如图3,作弦CH,连接DH,∠CDH=3∠EDH,CH=2 ![]() ,BE=4
,BE=4 ![]() ,求DH的长.
,求DH的长. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=2,∠ABC=60°,对角线AC、BD相交于点O,将对角线AC所在的直线绕点O顺时针旋转角α(0°<α<90°)后得直线l,直线l与AD、BC两边分别相交于点E和点F. 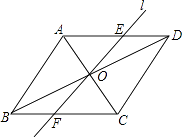
(1)求证:△AOE≌△COF;
(2)当α=30°时,求线段EF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋中装有20个只有颜色不同的球,其中5个黄球,8个黑球,7个红球.
(1)求从袋中摸出一个球是黄球的概率;
(2)现从袋中取出若干个黑球,搅匀后,使从袋中摸出一个球是黑球的概率是 ![]() ,求从袋中取出黑球的个数.
,求从袋中取出黑球的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1为平地上一幢建筑物与铁塔图,图2为其示意图.建筑物AB与铁塔CD都垂直于地面,BD=30m,在A点测得D点的俯角为45°,测得C点的仰角为60°.求铁塔CD的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a>0)过(﹣2,0),(2,3)两点,那么抛物线的对称轴( )
A.只能是x=﹣1
B.可能是y轴
C.可能在y轴右侧且在直线x=2的左侧
D.可能在y轴左侧且在直线x=﹣2的右侧
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com