
【题目】如图,已知AB=AC=AD,且AD∥BC,求证:∠C=2∠D.
【答案】证明:∵AB=AC=AD,
∴∠C=∠ABC,∠D=∠ABD,
∴∠ABC=∠CBD+∠D,
∵AD∥BC,
∴∠CBD=∠D,
∴∠ABC=∠D+∠D=2∠D,
又∵∠C=∠ABC,
∴∠C=2∠D.
【解析】首先根据AB=AC=AD,可得∠C=∠ABC,∠D=∠ABD,∠ABC=∠CBD+∠D;然后根据AD∥BC,可得∠CBD=∠D,据此判断出∠ABC=2∠D,再根据∠C=∠ABC,即可判断出∠C=2∠D.
【考点精析】解答此题的关键在于理解平行线的性质的相关知识,掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补,以及对等腰三角形的性质的理解,了解等腰三角形的两个底角相等(简称:等边对等角).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知△ABC中,∠A=90°,AB=AC,D为BC的中点.
(1)如图,若E、F分别是AB、AC上的点,且BE=AF.求证:△DEF为等腰直角三角形; 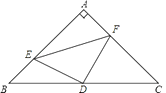
(2)若E,F分别为AB,CA延长线上的点,仍有BE=AF,其他条件不变,那么△DEF是否仍为等腰直角三角形?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将代数式x2+6x+2化成(x+p)2+q的形式为( )
A. (x-3)2+11 B. (x+3)2-7 C. (x+3)2-11 D. (x+2)2+4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,AC⊥BC,AE为∠BAC的平分线,DE⊥AB,AB=7cm,AC=3cm,则BD等于( ) 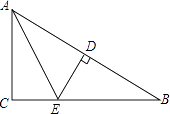
A.1cm
B.2cm
C.3cm
D.4cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABC≌△DEC,∠ACB=60°,∠BCD=100°,点A恰好落在线段ED上,则∠B的度数为( ) 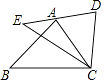
A.50°
B.60°
C.55°
D.65°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】杨阳同学沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙O,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语,其具体信息汇集如下: 如图,AB∥OH∥CD,相邻两平行线间的距离相等,AC,BD相交于O,OD⊥CD.垂足为D,已知AB=20米,请根据上述信息求标语CD的长度.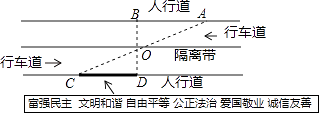
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校有25名同学参加某项比赛,预赛成绩各不相同,取前13名参加决赛,其中一名同学已经知道自己的成绩,能否进入决赛,只需要再知道这25名同学成绩的()
A. 最高分 B. 中位数 C. 方差 D. 平均数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(1,2),B(3,1),C(﹣2,﹣1). 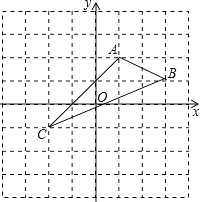
(1)在图中作出△ABC关于y轴对称的△A1B1C1 .
(2)写出A1 , B1 , C1的坐标(直接写出答案),
A1;B1;C1 .
(3)△A1B1C1的面积为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com